题目内容
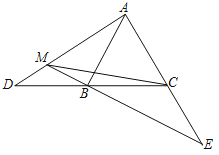
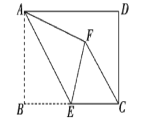
【题目】如图,在正方形![]() 中,
中,![]() ,
,![]() 与
与![]() 相交于点
相交于点![]() ,
,![]() 是
是![]() 的中点,点
的中点,点![]() 在
在![]() 边上,且
边上,且![]() ,
,![]() 为对角线
为对角线![]() 上一点,当对角线
上一点,当对角线![]() 平分
平分![]() 时,
时,![]() 的值为( )
的值为( )
A.1B.![]() C.2D.
C.2D.![]()
【答案】A
【解析】
过点M作NH⊥BD于点H,设PH=x,易得BH=HM=![]() ,BO=
,BO=![]() ,HO=
,HO=![]() ,ON=
,ON=![]() ,由tan∠OPN=tan∠MPH,得
,由tan∠OPN=tan∠MPH,得![]() ,分两类情况:①当点P在线段BH上时,②当点P在线段DH上时,分别列出方程,求出x的值,进而求出答案.
,分两类情况:①当点P在线段BH上时,②当点P在线段DH上时,分别列出方程,求出x的值,进而求出答案.
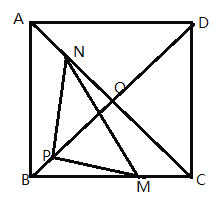
过点M作NH⊥BD于点H,设PH=x,
∵在正方形![]() 中,
中,
∴∠OBC=45°,即:BOC和HBM是等腰直角三角形,
∵![]() ,BC=
,BC=![]() ,
,
∴BH=HM=3÷![]() =
=![]() ,BO=4÷
,BO=4÷![]() =
=![]() ,
,
∴HO=![]() -
-![]() =
=![]() ,
,
∵![]() 是
是![]() 的中点,
的中点,
∴ON=![]() OA=
OA=![]() OB=
OB=![]() ,
,
∵对角线![]() 平分
平分![]() ,
,
∴tan∠OPN=tan∠MPH,
∴![]() ,
,
①当点P在线段BH上时,如图1,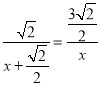 ,解得:x=
,解得:x=![]() (舍去),
(舍去),
②当点P在线段DH上时,如图2, ,解得:x=
,解得:x=![]() ,
,
∴PH=![]() ,OP=
,OP=![]() -
-![]() =
=![]() ,
,
∴PN=![]() ,
,
PM=![]() ,
,
∴![]() =
=![]() ,
,
故选A
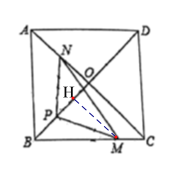
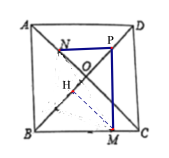
图1 图2

练习册系列答案
相关题目
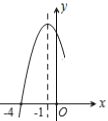
【题目】有这样一个问题:探究函数y=![]() 的图象与性质.小美根据学习函数的经验,对函数y=
的图象与性质.小美根据学习函数的经验,对函数y=![]() 的图象与性质进行了探究下面是小美的探究过程,请补充完整:
的图象与性质进行了探究下面是小美的探究过程,请补充完整:
(1)函数y=![]() 的自变量x的取值范围是 ;
的自变量x的取值范围是 ;
(2)下表是y与x的几组对应值.
x | -2 | - | -1 | - |
|
| 1 | 2 | 3 | 4 | … |
y | 0 | - | -1 | - |
|
|
| m |
|
| … |
求m的值;
(3)如图,在平面直角坐标系xOy中,描出了以上表中各对对应值为坐标的点.根据描出的点,画出该函数的图象;
(4)结合函数的图象,写出该函数的一条性质: .