Question

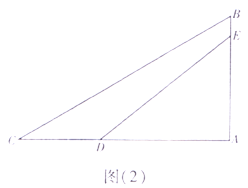
【题目】如图，在平面直角坐标系中，已知矩形AOBC的顶点C的坐标是（2，4），动点P从点A出发，沿线段AO向终点O运动，同时动点Q从点B出发，沿线段BC向终点C运动．点P、Q的运动速度均为每秒1个单位，过点P作PE⊥AO交AB于点E，一点到达，另一点即停．设点P的运动时间为t秒（t＞0）．

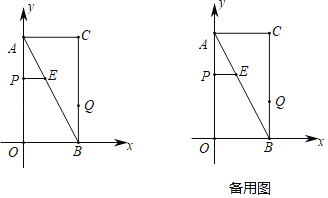
（1）填空：用含t的代数式表示下列各式：AP＝______，CQ＝_______．

（2）①当PE＝时，求点Q到直线PE的距离．

②当点Q到直线PE的距离等于时，直接写出t的值．

（3）在动点P、Q运动的过程中，点H是矩形AOBC（包括边界）内一点，且以B、Q、E、H为顶点的四边形是菱形，直接写出点H的横坐标．

Answer 1

【答案】（1）t，4﹣t；（2）①点Q到直线PE的距离为2；②t的值为秒或秒；（3）点H的横坐标为或10﹣4．

【解析】

（1）由点C坐标及矩形的性质可得出OA＝BC＝4，OB＝AC＝2，AO⊥OB，由题意得AP＝t，BQ＝t，得出CQ＝BC﹣BQ＝4﹣t；

（2）①延长PE交BC于F，则PF⊥BC，CF＝AP＝t，由PE⊥AO可得四边形APFC是矩形，可证明PE//OB，可得△APE∽△AOB，得出，解得t＝1，得出BQ＝1，CF＝1，CQ＝3，求出FQ＝CQ﹣CF＝2即可；

②延长PE交BC于F，则PF⊥BC，CF＝AP＝t，当Q在P的下方时，由题意得t++t＝4，解得t＝；当Q在P的上方时，由题意得t+t-＝4，解得t＝．

（3）由PE//OB，可得△APE∽△AOB，根据相似三角形的性质可求出E（t，4﹣t），Q（2，t），①当QE＝BQ时，延长PE交BC于F，则PF⊥BC，CF＝AP＝t，则（2﹣t）2+（4﹣2t）2＝t2，解得t＝，或t＝4（舍去），得出t＝即可；

②当BQ＝EB时，则BE＝BQ＝t，利用勾股定理可得AB=2，由△APE∽△AOB，得出＝，求出AE＝t，得出BE＝AB﹣AE＝2﹣t，解得t＝20﹣8，即可得出答案．

（1）∵矩形AOBC的顶点C的坐标是（2，4），

∴OA＝BC＝4，OB＝AC＝2，AO⊥OB，

∵点P、Q的运动速度均为每秒1个单位，

∴AP＝t，BQ＝t，

∴CQ＝BC﹣BQ＝4﹣t；

故答案为：t，4﹣t

（2）①如图1，延长PE交BC于F，

∵PE⊥OA，∠OAC=∠ACB=90°，

∴四边形APFC是矩形，

∴PF⊥BC，CF＝AP＝t，

∵PE⊥AO，AO⊥OB，

∴PE∥OB，

∴△APE∽△AOB，

∴＝，即，

解得：t＝1，

∴BQ＝1，CF＝1，

∴CQ＝4﹣1＝3，

∴FQ＝CQ﹣CF＝2；即点Q到直线PE的距离为2．

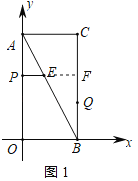
②延长PE交BC于F，则PF⊥BC，CF＝AP＝t，QF=，

①如上图1，当Q在P的下方时，

由题意得：CF+FQ+BQ=BC=4，即t++t＝4，

解得：t＝；

②当Q在P的上方时，如图2所示：

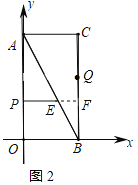
由题意得：BQ+CF-QF=BC，即t+t-=4，

解得：t＝，

∴当点Q到直线PE的距离等于时，t的值为秒或秒．

（3）∵PE⊥AO，AO⊥OB，

∴PE∥OB，

∴△APE∽△AOB，

∴，即，

解得：PE＝t，

∵OP＝4﹣t，

∴E（t，4﹣t），Q（2，t），

①如图3，当QE＝BQ时，四边形EQBH是菱形，EH//BQ//y轴，

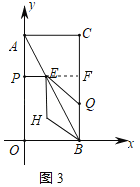
延长PE交BC于F，则PF⊥BC，CF＝AP＝t，FQ=BC-CF-BQ=4-2t，EF=PF-PE=2-t，

∴（2﹣t）2+（4﹣2t）2＝t2，

解得：t＝，或t＝4（舍去），

∴t＝，

∵EH//BQ//y轴，

∴点H的横坐标为，

②如图4，当BQ＝EB时，四边形BQHE是菱形，则BE＝BQ＝t，EH//BQ//y轴，

∵∠AOB＝90°，OB＝2，OA＝4，

∴AB＝＝2，

∵△APE∽△AOB，

∴，即

∴AE＝t，

∴BE＝AB﹣AE＝2﹣t，

∴2﹣t＝t，

解得：t＝20﹣8，

∴t＝4＝10﹣4，

∵EH//BQ//y轴，

∴点H的横坐标为10﹣4，

综上所述，点H的横坐标为或10﹣4．