题目内容
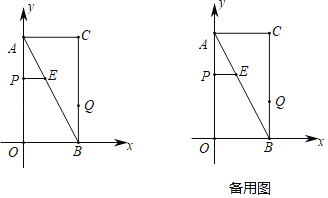
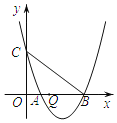
【题目】如图,抛物线y=![]() x+3与x轴交于A、B两点(点A在点B的左侧),与y轴交于点C,点Q是线段OB上一动点,连接BC,点M在线段BC上,且使△BQM为直角三角形的同时△CQM为等腰三角形,则此时点Q的横坐标为( )
x+3与x轴交于A、B两点(点A在点B的左侧),与y轴交于点C,点Q是线段OB上一动点,连接BC,点M在线段BC上,且使△BQM为直角三角形的同时△CQM为等腰三角形,则此时点Q的横坐标为( )
A.![]() 或
或![]() B.
B.![]() 或
或![]() C.
C.![]() 或
或![]() D.
D.![]() 或
或![]()
【答案】C
【解析】
先求得A、B、C的坐标,即可求得AB的长,求得直线BC的解析式,然后分两种情况分别讨论①当∠BQM=90°时,设M(a,b),由△MQB∽△COB,得![]() ,列出方程即可.②当∠QMB=90°时,设CM=MQ=m,则BM=5-m,由△BMQ∽△BOC,可得
,列出方程即可.②当∠QMB=90°时,设CM=MQ=m,则BM=5-m,由△BMQ∽△BOC,可得![]() ,解方程即可.
,解方程即可.
抛物线y=![]() x+3与x轴交于A、B两点(点A在点B的左侧),与y轴交于点C,
x+3与x轴交于A、B两点(点A在点B的左侧),与y轴交于点C,
∴令y=0,则![]() x+3=0,解得x=1或4,
x+3=0,解得x=1或4,
∴A(1,0),B(4,0),
令x=0,则y=3,
∴C(0,3),
∴OB=4,OC=3,
∴BC=![]() =5;
=5;
①当∠BQM=90°时,如图1,设M(a,b),
∵∠CMQ>90°,
∴只能CM=MQ=b,
∵MQ∥y轴,
∴△MQB∽△COB,
∴![]() ,即
,即 ![]() ,解得b=
,解得b=![]()
∴点Q的横坐标为![]() ;
;
②当∠QMB=90°时,如图2,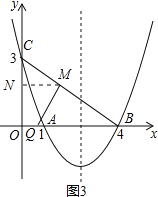
∵∠CMQ=90°,
∴只能CM=MQ,
设CM=MQ=m,
∴BM=5-m,
∵∠BMQ=∠COB=90°,∠MBQ=∠OBC,
∴△BMQ∽△BOC,
∴![]() ,解得m=
,解得m=![]() ,
,
∴BM=BC-CM=5-![]() =
=![]() ,
,
∵∠BMQ=∠BOC=90°,∠ABM=∠OBC,
∴△QMB∽△COB,
∴![]() ,即
,即 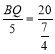 ,
,
∴BQ=![]() ,
,
∴OQ=OB-BQ=4-![]() =
=![]()
∴点Q的横坐标为![]() ,
,
综上,点Q的横坐标为![]() 或
或![]() ,
,
故选:C.

【题目】某水果批发市场规定,批发苹果不少于![]() 时,批发价为5元/
时,批发价为5元/![]() .小王携带现金4000元到这市场采购苹果,并以批发价买进.
.小王携带现金4000元到这市场采购苹果,并以批发价买进.
(Ⅰ)根据题意,填表:
购买数量 |
|
|
|
|
花费 |
|
| ||
剩余现金 |
|
|
(Ⅱ)设购买的苹果为![]() ,小王付款后还剩余现金
,小王付款后还剩余现金![]() 元.求
元.求![]() 关于
关于![]() 的函数解析式,并指出自变量
的函数解析式,并指出自变量![]() 的取值范围;
的取值范围;
(Ⅲ)根据题意填空:若小王剩余现金为700元,则他购买__________![]() 的苹果.
的苹果.
【题目】某校为激发学生学习数学的兴趣,开设了“数独、速算、魔方、七巧板、华容道”五门校本课程,规定每位学生只能选一门.该校共有学生1600人.为了解学生的报名意向,学校随机调查了一些学生,并制成如下统计图表:
校本课程报名意向统计表
课程 | 频数 | 频率 |
数独 | 8 | a |
速算 | m | 0.2 |
魔方 | 27 | b |
七巧板 | n | 0.3 |
华容道 | 15 | c |
(1)在这次活动中,学校采取的调查方式是 (填写“普查”或“抽样调查”);
(2)求出扇形统计图中“速算”所对应的扇形圆心角的度数;
(3)a+b+c= ,m= ;(答案直接填写在横线上)
(4)请你估算,全校选择“数独”和“魔方”的学生共有多少人?

【题目】 贫困户老王在精准扶贫工作队的帮扶下,在一片土地上种植了优质水果蓝莓,经核算,种植成本为18元/千克.今年正式上市销售,通过30天的试销发现:第1天卖出20千克;以后每天比前一天多卖4千克,销售价格![]() 元/千克)与时间x(天)之间满足如下表:
元/千克)与时间x(天)之间满足如下表:
时间 | (1≤x<20) | (20≤x≤30) |
销售价格y(元/千克) | -0.5x+38 | 25 |
(其中,x,y均为整数)
(1)试销中销售量P(千克)与时间![]() (天)之间的函数关系式为 .
(天)之间的函数关系式为 .
(2)求销售蓝莓第几天时,当天的利润w最大?最大利润是多少元?
(3)求试销的30天中,当天利润w不低于870元的天数共有几天.