题目内容
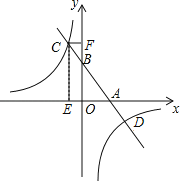
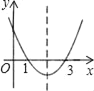
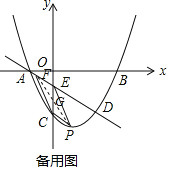
【题目】如图,抛物线![]() 经过点B(3,0),C(0,-2),直线L:
经过点B(3,0),C(0,-2),直线L:![]() 交y轴于点E,且与抛物线交于A,D两点,P为抛物线上一动点(不与A重合).
交y轴于点E,且与抛物线交于A,D两点,P为抛物线上一动点(不与A重合).
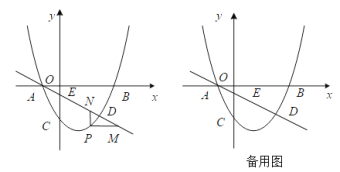
(1)求抛物线的解析式.
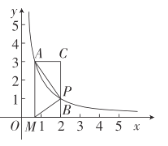
(2)当点P在直线L下方时,过点P作PM∥x轴交L于点M,PN∥y轴交L于点N,求PM+PN的最大值.
(3)设F为直线L上的点,以E,C,P,F为顶点的四边形能否构成平行四边形?若能,求出点F的坐标;若不能,请说明理由.
【答案】(1)![]() ;(2)
;(2)![]() ;
;
(3)能,
【解析】
(1)把B(3,0),C(0,-2)代入![]() 解方程组即可得到结论;
解方程组即可得到结论;
(2)设![]() ,
,
得到![]() ,
,![]() ,根据二次函数的性质即可得到结论;
,根据二次函数的性质即可得到结论;
(3)求得![]() ,得到
,得到![]() ,设
,设![]() ,①以CE为边,根据CE=PF,列方程得到m=1,m=0(舍去),②以CE为对角线,连接PF交CE于G,CG=GE,PG=FG,得到
,①以CE为边,根据CE=PF,列方程得到m=1,m=0(舍去),②以CE为对角线,连接PF交CE于G,CG=GE,PG=FG,得到![]() ,设
,设![]() ,则
,则![]() ,列方程得到此方程无实数根,于是得到结论.
,列方程得到此方程无实数根,于是得到结论.
(1)把B(3,0),C(0,-2)代入![]() 得,
得,
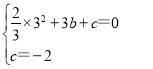 ,
,
∴ ,
,
∴抛物线的解析式为:![]() ;
;
(2)设![]() ,
,
∵PM∥x轴,PN∥y轴,M,N在直线AD上,
∴![]() ,
,![]() ,
,
∴![]()
![]() ,
,
∴当![]() 时,PM+PN的最大值是
时,PM+PN的最大值是![]() ;
;
(3)能,
理由:∵![]() 交y轴于点E,
交y轴于点E,
∴![]() ,
,
∴![]() ,
,
设![]() ,
,
若以E,C,P,F为顶点的四边形能构成平行四边形,
①以CE为边,∴CE∥PF,CE=PF,
∴![]() ,
,
∴![]() 或
或![]()
∴m1=1,m2=0(舍去),![]() ,
,
 ;
;
以CE为对角线,连接PF交CE于G,
∴CG=GE,PG=FG,
∴![]() ,
,
设![]() ,则
,则![]() ,
,
∴![]() ,
,
∴m=1,m=0(舍去),
∴![]() ,
,
综上所述,
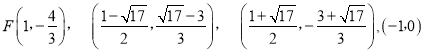 ,
,
以E,C,P,F为顶点的四边形能构成平行四边形.

 学期复习一本通学习总动员期末加暑假延边人民出版社系列答案
学期复习一本通学习总动员期末加暑假延边人民出版社系列答案 芒果教辅暑假天地重庆出版社系列答案
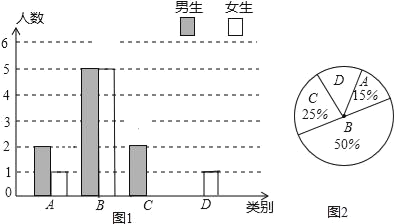
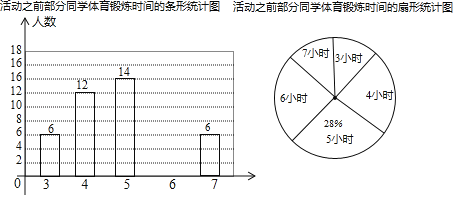
芒果教辅暑假天地重庆出版社系列答案【题目】重庆一中开展了“爱生活爱运动”的活动,以鼓励学生积极参与体育锻炼.为了解学生每周体育锻炼时间,学校在活动之前对八年级同学进行了抽样调査,并根据调査结果将学生每周的体育锻炼时间分为3小时、4小时、5小时、6小时、7小时共五种情况.小明根据调查结构制作了如图两幅统计图,请你结合图中所给信息解答下列问题:
(整理数据)
“爱生活爱运动”的活动结束之后,再次抽查这部分学生的体育锻炼时间:
一周体育锻炼时间(小时) | 3 | 4 | 5 | 6 | 7 |
人数 | 3 | 5 | 15 | a | 10 |
活动之后部分学生体育锻炼时间的统计表
(分析数据)
平均数 | 中位数 | 众数 | |
活动之前锻炼时间(小时) | 5 | 5 | 5 |
活动之后锻炼时间(小时) | 5.52 | b | c |
请根据调查信息
(1)补全条形统计图,并计算a= ,b= 小时,c= 小时;
(2)小亮同学在活动之前与活动之后的这两次调查中,体育锻炼时间均为5小时,根据体育锻炼时间由多到少进行排名统计,请问他在被调查同学中体育锻炼时间排名靠前的是 (填“活动之前”或“活动之后”),理由是 ;
(3)已知八年级共2200名学生,请估算全年级学生在活动结束后,每周体育锻炼时间至少有6小时的学生人数有多少人?