题目内容
【题目】正方形
的边长为
，点
分别是线段
上的动点，连接
并延长，交边
于
，过
作
，垂足为
，交边
于点
．
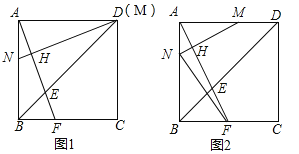
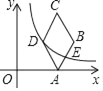
（1）如图1，若点与点
重合，求证：
；
（2）如图2，若点从点出发，以
的速度沿
向点
运动，同时点
从点
出发，以
的速度沿
向点运动，运动时间为
．
①设
,求
关于
的函数表达式；
②当
时，连接
，求的长．
【答案】（1）见解析；（2）①
；②
．
【解析】
（1）根据正方形的性质得到
，
，由垂直的定义得到
，由余角的性质得到
，根据全等三角形的性质即可得到结论；
（2）①根据勾股定理得到
，由题意得，
，
，求得
，
，根据相似三角形的判定和性质即可得到结论；
②根据已知条件得到
，
，根据相似三角形的性质得到
，由①求得
，得方程
，求出
，进而求出
，利用勾股定理得到结论．
解：（1）
四边形
是正方形，
，，
，
，
，
，
在
与
中，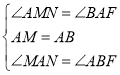
，
，
；
（2）①
，
，
由题意得，，，
，，
，
，
，即
，
；
②
，
，，
由（1）证得
，
，
，
，即
，
，
由①求得，
，
，
，
在
中
．
练习册系列答案
寒假创新型自主学习第三学期寒假衔接系列答案
相关题目
