��Ŀ����
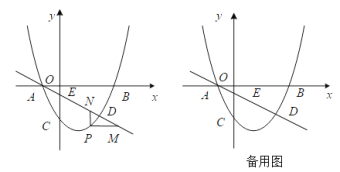
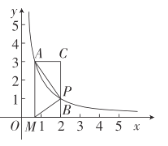
����Ŀ����ͼ����ƽ��ֱ������ϵ�У���A(![]() ��3)�ڷ���������C��y=
��3)�ڷ���������C��y=![]() (x>0)�ϣ���P�Ƿ���������C��y=
(x>0)�ϣ���P�Ƿ���������C��y=![]() (x>0)��-���㣬����AP����M��x���ϣ�������MP��AP������ΪP��
(x>0)��-���㣬����AP����M��x���ϣ�������MP��AP������ΪP��
(1)���������Ľ���ʽ��
(2)����P(2��n)����PM����ֱ�ߵĽ���ʽ��
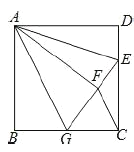
(3)PB��x�ᣬBΪ���㣬CA��y�ᣬBP���ӳ��߽�AC�ڵ�C������AMP����APC����ʱ����д����AMP���BMP��������ϵ����˵�����ɣ�
���𰸡���1��y=![]() ����2��y=
����2��y=![]() x��
x��![]() ����3����AMP=��BMP���AMP+��BMP=90�������ɼ�������
����3����AMP=��BMP���AMP+��BMP=90�������ɼ�������
��������
��1��k=![]() ��3=2���ʷ����������Ľ���ʽΪ��y=
��3=2���ʷ����������Ľ���ʽΪ��y=![]() ��
��
��2���������P�����꣬Ȼ��õ���C�����꣬��֤����APC����PMB���õ���M�����꣬���ݴ���ϵ�������������ֱ�ߵĽ���ʽ.
��3���������������ε����ʣ��ֳ���������������ۣ����ɵõ���.
�⣺��1����k=![]() ��3=2��
��3=2��
�෴���������Ľ���ʽΪ��y=![]() ��
��
(2)��P��2��n���ڷ���������C��y=![]() (x>0)��ͼ���ϣ�
(x>0)��ͼ���ϣ�
��n=1��
��P(2��1)��
��PB��x�ᣬMP��AP��CA��y�ᣬ
��C(2��3)����C=��APM=��MBP=90����
���APC����MPB=90������PMB����MPB=90��
���APC=��PMB��
����APC����PMB
��![]() =
=![]() ��
��
��MB=![]() ��M(
��M(![]() ��0)
��0)
��PM����ֱ�ߵĽ���ʽΪ��y=kxʮb��
��P(2��1)��M(![]() ��0)����ã�
��0)����ã�
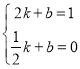 ��
��
��ã�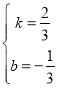 ��
��
��y=![]() x��
x��![]() ��
��
(3)����AMP����APC����ʱ���֡���APC����PMB��
��������������PMB���ƣ�
���AMP=��BMP���AMP=��PBM��
���AMP=��BMP���AMP+��BMP=90����

 ��ѧȫ��������ѵ��ϵ�д�
��ѧȫ��������ѵ��ϵ�д�