题目内容
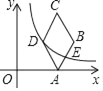
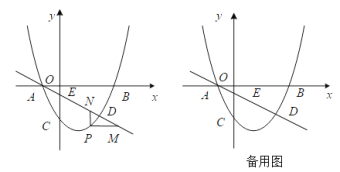
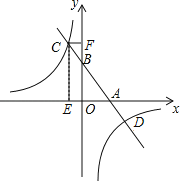
【题目】如图,已知一次函数y=kx+b的图象与x轴,y轴分别相交于A,B两点,且与反比例函数y=![]() 交于点C,D.作CE⊥x轴,垂足为E,CF⊥y轴,垂足为F.点B为OF的中点,四边形OECF的面积为16,点D的坐标为(4,﹣b).
交于点C,D.作CE⊥x轴,垂足为E,CF⊥y轴,垂足为F.点B为OF的中点,四边形OECF的面积为16,点D的坐标为(4,﹣b).
(1)求一次函数表达式和反比例函数表达式;
(2)求出点C坐标,并根据图象直接写出不等式kx+b≤![]() 的解集.
的解集.
【答案】(1)y=﹣2x+4;(2)﹣2≤x<0或x≥4.
【解析】
(1)由矩形的面积求得m=﹣16,得到反比例函数的解析式,把D(4,﹣b)代入求得的解析式得到D(4,﹣4),求得b=4,把D(4,﹣4)代入y=kx+4,即可求得一次函数的解析式;
(2)由一次函数的解析式求得B的坐标为(0,4),根据题意OF=8,C点的纵坐标为8,代入反比例函数的解析式求得横坐标,得到C的坐标,根据C、D的坐标结合图象即可求得不等式kx+b≤![]() 的解集.
的解集.
解:(1)∵CE⊥x轴,CF⊥y轴,
∵四边形OECF的面积为16,
∴|m|=16,
∵双曲线位于二、四象限,
∴m=﹣16,
∴反比例函数表达式为y=![]() ,
,
将x=4代入y=![]() 得:y=﹣4,
得:y=﹣4,
∴D(4,﹣4),
∴b=4
将D(4,﹣4)代入y=kx+4,得k=﹣2
∴一次函数的表达式为y=﹣2x+4;
(2)∵y=﹣2x+4,
∴B(0,4),
∴OF=8,
将y=8代入y=﹣2x+4得x=﹣2,
∴C(﹣2,8),
∴不等式kx+b≤![]() 的解集为﹣2≤x<0或x≥4.
的解集为﹣2≤x<0或x≥4.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目