题目内容
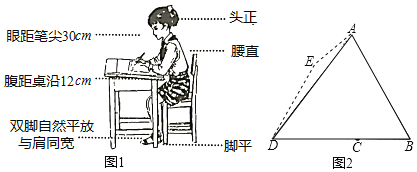
【题目】我们知道良好的坐姿有利于青少年骨骼生长，有利于身体健康，那么首先要有正确的写字坐姿，身子上半部坐直，头部端正、目视前方，两手放在桌面上，两腿平放，胸膛挺起，理想状态下，如图1所示，将图1中的眼睛记为点A，腹记为点B，笔尖记为点D，且BD与桌沿的交点记为点C
（1）若∠ADB＝53°，∠B＝60°，求A到BD的距离及C、D两点间的距离（结果精确到1cm）．
（2）老师发现小红同学写字姿势不正确，眼睛倾斜至图2的点E，点E正好在CD的垂直平分线上，且∠BDE＝60°，于是要求其纠正为正确的姿势．求眼睛所在的位置应上升的距离．（结果精确到1cm）
参考数据：sin53°≈0.80，cos53°≈0.60，．tan53°≈1.33，
≈1.41，
≈1.73）
【答案】（1）A到BD的距离为24cm，C、D两点间的距离为20cm；（2）眼睛所在的位置应上升的距离为7cm．
【解析】
（1）由图1知AD=30cm，BC=12cm，过A作
于H，则
，解直角三角形即可得到A到BD的距离
的长，及BH的长；而CD=AH+BH-BC；
（2）过E作
，过A作
交GE的延长线于F，得到四边形AFGH是矩形，求得
，根据线段垂直平分线的性质得到
，解直角三角形即可得到结论．
解：（1）过A作AH⊥BD于H（见下图），
则∠AHD=∠AHB＝90°，
又∵由图1得AD＝30，∠ADB＝53°，
∴AH＝ADsin53°＝30×0.80≈24，DH＝ADcos53°＝30×0.60＝18，
又∵∠B=60°，
∴BH=
≈14，
∴BD=BH+DH=32，
又∵由图1得BC=12，
∴CD=32﹣12=20，
答：A到BD的距离为24cm，C、D两点间的距离为20cm；
（2）过E作EG⊥CD，
过A作AF⊥EG交GE的延长线于F，
则四边形AFGH是矩形，
∴FG＝AH＝24，
∵点E正好在CD的垂直平分线上，
∴DG＝
CD＝10，
∵∠EDC＝60°，
∴EG＝
DG＝10≈17.3，
∴EF＝FG﹣EG≈7cm，
答：眼睛所在的位置应上升的距离为7cm．
