题目内容
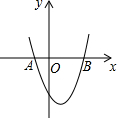
设函数y=x2-(2k+1)x+2k-4的图象如图所示,它与x轴交于A,B两点,且线段OA与OB的长度之比为1:3,则k=______.

y=x2-(2k+1)x+2k-4,令y=0,得到x2-(2k+1)x+2k-4=0,
设A(a,0),B(b,0),
可得x2-(2k+1)x+2k-4=0的两个解分别为a,b(a<0,b>0),
则有a+b=2k+1,ab=2k-4,
又线段OA与OB的长度之比为1:3,即-a:b=1:3,
∴b=-3a,
∴a-3a=2k+1,a•(-3a)=2k-4,即a=-
(2k+1)=-k-
①,-3a2=2k-4②,
①代入②消去a得:-3(-k-
)2=2k-4,即12k2+20k-13=0,
分解因式得:(2k-1)(6k+13)=0,
解得:k=
或k=-
,
∵抛物线开口向上,且对称轴在y轴右边,
∴-(2k+1)<0,即k>-
,故k=-
舍去,
∴k=
.
故答案为:
设A(a,0),B(b,0),
可得x2-(2k+1)x+2k-4=0的两个解分别为a,b(a<0,b>0),
则有a+b=2k+1,ab=2k-4,
又线段OA与OB的长度之比为1:3,即-a:b=1:3,
∴b=-3a,
∴a-3a=2k+1,a•(-3a)=2k-4,即a=-
| 1 |
| 2 |
| 1 |
| 2 |
①代入②消去a得:-3(-k-
| 1 |
| 2 |
分解因式得:(2k-1)(6k+13)=0,
解得:k=
| 1 |
| 2 |
| 13 |
| 6 |
∵抛物线开口向上,且对称轴在y轴右边,
∴-(2k+1)<0,即k>-
| 1 |
| 2 |
| 13 |
| 6 |
∴k=
| 1 |
| 2 |
故答案为:
| 1 |
| 2 |

练习册系列答案
相关题目


