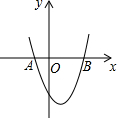
题目内容
已知抛物线y=x2-2x-3与x轴相交于A、B两点，抛物线上有一点P，且△ABP的面积为6．
（1）求A与B的坐标；
（2）求点P的坐标．
（1）求A与B的坐标；
（2）求点P的坐标．
（1）∵y=x2-2x-3=（x+1）（x-3）
∴A（-1，0），B（3，0）；
（2）设点P的坐标是（x，y）．则由题意，得
S△ABP=
AB•|y|=
×4•|y|=6，
解得，|y|=3．
①当y=-3时，当y=3时，x2-2x-3=-3，即x2-2x=0，
解得x1=，x2=2．则P1（0，-3），P2（2，-3）；
②当y=3时，x2-2x-3=3，即x2-2x-6=0，
解得x1=1+
，x2=1-
；
则P3(1+
，3)，P4(1-
，3)．
综上所述，符号条件的点P的坐标分别是：P1（0，-3），P2（2，-3），P3(1+
，3)，P4(1-
，3)．
∴A（-1，0），B（3，0）；
（2）设点P的坐标是（x，y）．则由题意，得
S△ABP=
| 1 |
| 2 |
| 1 |
| 2 |
解得，|y|=3．
①当y=-3时，当y=3时，x2-2x-3=-3，即x2-2x=0，
解得x1=，x2=2．则P1（0，-3），P2（2，-3）；
②当y=3时，x2-2x-3=3，即x2-2x-6=0，
解得x1=1+
| 7 |
| 7 |
则P3(1+
| 7 |
| 7 |
综上所述，符号条件的点P的坐标分别是：P1（0，-3），P2（2，-3），P3(1+
| 7 |
| 7 |
练习册系列答案
名师伴你成长课时同步学练测系列答案
相关题目
B两点，如图．
