题目内容
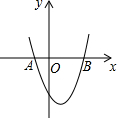
已知抛物线y=-
x2+(6-
)x+m-3与x轴有A、B两个交点,且A、B两点关于y轴对称.
(1)求m的值;
(2)写出抛物线解析式及顶点坐标;
(3)根据二次函数与一元二次方程的关系,将此题的条件换一种说法写出来.
| 1 |
| 2 |
| m2 |
(1)求m的值;
(2)写出抛物线解析式及顶点坐标;
(3)根据二次函数与一元二次方程的关系,将此题的条件换一种说法写出来.
(1)设A(x1,0)B(x2,0).
∵A、B两点关于y轴对称,
∴6-
=0,
∴m=±6.
当m=-6时,此方程无实数根,应舍去.
∴m=6;
(2)求得y=-
x2+3.顶点坐标是(0,3);
(3)方程-
x2+(6-
)x+m-3=0的两根互为相反数(或两根之和为零等).
∵A、B两点关于y轴对称,
∴6-
| m2 |
∴m=±6.
当m=-6时,此方程无实数根,应舍去.
∴m=6;
(2)求得y=-
| 1 |
| 2 |
(3)方程-
| 1 |
| 2 |
| m2 |

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目