题目内容
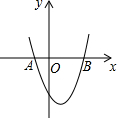
如图，抛物线y=-x2+2（m+1）x+m+3与x轴交于A，B两点，若OA：OB=3：1，求m的值．______．
设B（-k，0），则A（3k，0）．
∴-k，3k是方程-x2+2（m+1）x+m+3=0的两根，
∴
．
解得：m=0或-
，
∵都满足△＞0，
如图：若x1，x2是方程-x2+2（m+1）x+m+3=0的两根，
则x1•x2=-（m+3）＜0，x1+x2=2（m+1）＞0，
当m=-
时，x1+x2=2（m+1）=-
＜0，
∴m=-
不合题意，舍去．
∴m=0．
∴-k，3k是方程-x2+2（m+1）x+m+3=0的两根，
∴
|
解得：m=0或-
| 5 |
| 3 |
∵都满足△＞0，
如图：若x1，x2是方程-x2+2（m+1）x+m+3=0的两根，
则x1•x2=-（m+3）＜0，x1+x2=2（m+1）＞0，
当m=-
| 5 |
| 3 |
| 4 |
| 3 |
∴m=-
| 5 |
| 3 |
∴m=0．
练习册系列答案
天天向上一本好卷系列答案
小学生10分钟应用题系列答案
相关题目
B两点，如图．
