��Ŀ����
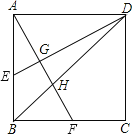
����Ŀ����ͼ������ABCD�ĶԽ������ж���E������DE����BC����һ����F������EF����֪AB=3cm��AD=4cm����A��E�����ľ���Ϊxcm��D��E�����ľ���Ϊy1cm��E��F�����ľ���Ϊy2cm.Сʤ����ѧϰ�����ľ��飬�ֱ�Ժ���y1��y2���Ա���x�ı仯���仯�Ĺ��ɽ�����̽��.
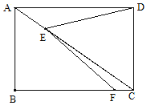
������Сʤ��̽�����̣��벹��������
��1�������±����Ա���x��ֵ����ȡ�㡢��ͼ���������õ�x��y�ļ����Ӧֵ��
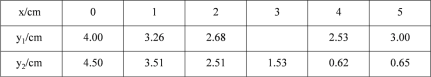
��2����ͬһƽ��ֱ������ϵxOy�У������ȫ��ı��и�����ֵ����Ӧ�ĵ㣨x��y1������x��y2��������������y1��y2��ͼ��
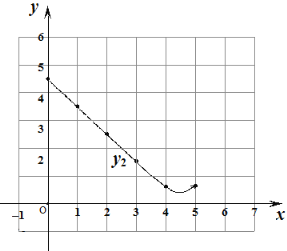
��3����Ϻ���ͼ������⣺��DE��EFʱ��AE�ij��ȷ�ΧԼΪ����cm��
���𰸡���1��2.41����2������ͼ�����������3����5��AE��1.68ʱ��DE��EF.
��������
��1��ֱ����ȷ����ͼ��ȡ������ɵ�����.
��2�������б�ֱ���������ƽ�����ߣ�
��3���ҵ�y1��y2�Ľ������꣬�����ж�.
(1) ȡ�㡢��ͼ���������õ�����Ϊ��x=3ʱ��y1=2.41
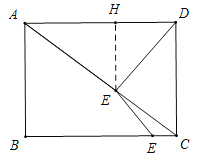
���㣺��EH��AD��
���ھ���ABCD��AD=4��AB=3��
��AC=5��
�ߡ�AHE�ס�ADC��
��![]() ��
��
����AE=3��
��EH=![]() ��AH=
��AH=![]() ��
��
��HD=![]()
��DE=![]() 1
1
��2���������
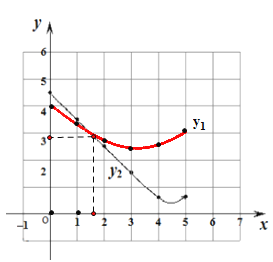
(3)���ͼ����Եó������Ľ�����x=1.68ʱ��y1=y2��
����5��x��1.68ʱ��y1��y2������5��AE��1.68ʱ��DE��EF.

 ��������ܸ�ϰϵ�д�
��������ܸ�ϰϵ�д�