题目内容
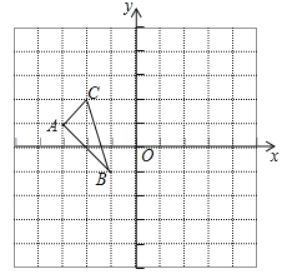
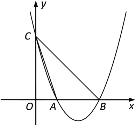
【题目】如图，二次函数y=x2+bx+c（c≠0）的图象经过点A（-2，m）（m＜0），与y轴交于点B，与x轴交于C、D两点（C在D的左侧），AB//x轴，且AB：OB=2：3．
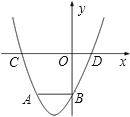
（1）求m的值；
（2）求二次函数的解析式；
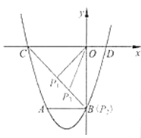
（3）在线段BC上是否存在点P，使ΔPOC为等腰三角形？若存在，求出点P的坐标；若不存在，请说明理由．
【答案】（1）m=-3;(2) 
;(3) 存在点
，
，
，使
为等腰三角形,理由见解析
【解析】
（1）由AB∥x轴，A（﹣2，m），可得AB=2，又由AB：OB=2：3，即可求得点B的坐标，则可求得m的值；
（2）由二次函数与y轴的交于点B，可求得c的值，又由图象过点A（﹣2，﹣3），将其代入函数解析式，即可求得b的值，则可得此二次函数解析式；
（3）由二次函数的图象与x轴交于C、D两点（点C在左恻），可得当y=0即可求得C的坐标，若△POC为等腰三角形，则可分别从①当PC=PO时，②当PO=CO时，③当PC=CO时去分析，即可求得满足条件的点P的坐标．
（1）∵AB∥x轴，A（﹣2，m），∴AB=2．
又∵AB：OB=2：3，∴OB=3，∴点B的坐标为（0，﹣3），∴m=﹣3；
（2）∵二次函数与y轴的交于点B，∴c=﹣3．
又∵图象过点A（﹣2，﹣3），∴﹣3=4﹣2b﹣3，∴b=2，∴二次函数解析式为y=x2+2x﹣3；
（3）当y=0时，有x2+2x﹣3=0，解得x1=﹣3，x2=1，由题意得：C（﹣3，0）．
若△POC为等腰三角形，则有：
①当PC=PO时，点P（
）；
②当PO=CO时，点P（0，﹣3）；
③当PC=CO时，设直线BC的函数解析式为y=kx+n，则有
，解得：
，∴直线BC的函数解析式为y=﹣x﹣3．
设点P（x，﹣x﹣3），由PC=CO，得：[﹣（x+3）]2+[﹣（﹣x﹣3）]2=32，解得：x1=﹣3
，x2=﹣3
（不合题意，舍去），∴P（﹣3
）．
综上所述：存在点P（）或P（0，﹣3）或P（﹣3），使△POC为等腰三角形．
