Ő‚ńŅńŕ»›
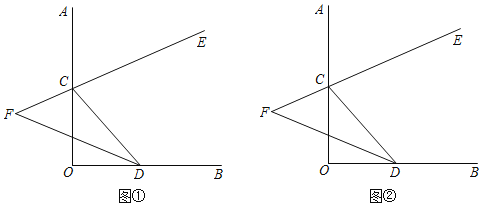
°ĺŐ‚ńŅ°Ņ»ÁÕľ£¨Ń‚–őABCDĶńĪŖ≥§ő™2cm£¨°ŌDAB=60°„£ģĶ„Pī”AĶ„≥Ų∑Ę£¨“‘![]() cm/sĶńňŔ∂»£¨—ōACŌÚC◊ų‘»ňŔ‘ň∂Į£Ľ”ŽīňÕ¨ Ī£¨Ķ„Q“≤ī”AĶ„≥Ų∑Ę£¨“‘1cm/sĶńňŔ∂»£¨—ō…šŌŖAB◊ų‘»ňŔ‘ň∂Į£ģĶĪP‘ň∂ĮĶĹCĶ„ Ī£¨P°ĘQ∂ľÕ£÷Ļ‘ň∂Į£ģ…ŤĶ„P‘ň∂ĮĶń Īľšő™ts£ģ
cm/sĶńňŔ∂»£¨—ōACŌÚC◊ų‘»ňŔ‘ň∂Į£Ľ”ŽīňÕ¨ Ī£¨Ķ„Q“≤ī”AĶ„≥Ų∑Ę£¨“‘1cm/sĶńňŔ∂»£¨—ō…šŌŖAB◊ų‘»ňŔ‘ň∂Į£ģĶĪP‘ň∂ĮĶĹCĶ„ Ī£¨P°ĘQ∂ľÕ£÷Ļ‘ň∂Į£ģ…ŤĶ„P‘ň∂ĮĶń Īľšő™ts£ģ
£®1£©ĶĪP“ž”ŕA£ģC Ī£¨«ŽňĶ√ųPQ°őBC£Ľ
£®2£©“‘Pő™‘≤–ń°ĘPQ≥§ő™įŽĺ∂◊ų‘≤£¨«Žő £ļ‘ŕ’ŻłŲ‘ň∂ĮĻż≥Ő÷–£¨tő™‘ű—ýĶń÷Ķ Ī£¨°—P”ŽĪŖBC∑÷Īū”–1łŲĻęĻ≤Ķ„ļÕ2łŲĻęĻ≤Ķ„£Ņ
°ĺīūįł°ŅĹ‚£ļ£®1£©°ŖňńĪŖ–őABCD «Ń‚–ő£¨«“Ń‚–őABCDĶńĪŖ≥§ő™2£¨
°ŗAB=BC=2£¨°ŌBAC=![]() °ŌDAB°£
°ŌDAB°£
”÷°Ŗ°ŌDAB=60°„£¨°ŗ°ŌBAC=°ŌBCA=30°„°£
»ÁÕľ1£¨Ń¨Ĺ”BDĹĽAC”ŕO°£
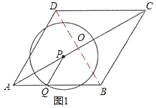
°ŖňńĪŖ–őABCD «Ń‚–ő£¨
°ŗAC°ÕBD£¨OA=![]() AC°£
AC°£
°ŗOB=![]() AB=1°£°ŗOA=
AB=1°£°ŗOA=![]() £¨AC=2OA=2
£¨AC=2OA=2![]() °£
°£
‘ň∂Įtsļů£¨AP=![]() t£¨AO=t£¨°ŗ
t£¨AO=t£¨°ŗ![]() °£
°£
”÷°Ŗ°ŌPAQ=°ŌCAB£¨°ŗ°ųPAQ°◊°ųCAB.°ŗ°ŌAPQ=°ŌACB.
°ŗPQ°őBC.
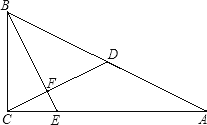
£®2£©»ÁÕľ2£¨°—P”ŽBC«–”ŕĶ„M£¨Ń¨Ĺ”PM£¨‘ÚPM°ÕBC°£
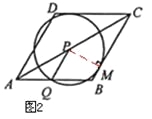
‘ŕRt°ųCPM÷–£¨°Ŗ°ŌPCM=30°„£¨°ŗPM=![]() °£
°£
”…PM=PQ=AQ=t£¨ľī![]() =t£¨Ĺ‚Ķ√t=
=t£¨Ĺ‚Ķ√t=![]() £¨
£¨
īň Ī°—P”ŽĪŖBC”–“ĽłŲĻęĻ≤Ķ„°£
»ÁÕľ3£¨°—PĻżĶ„B£¨īň ĪPQ=PB£¨
°Ŗ°ŌPQB=°ŌPAQ+°ŌAPQ=60°„
°ŗ°ųPQBő™Ķ»ĪŖ»żĹ«–ő°£°ŗQB=PQ=AQ=t°£°ŗt=1°£
°ŗĶĪ![]() Ī£¨°—P”ŽĪŖBC”–2łŲĻęĻ≤Ķ„°£
Ī£¨°—P”ŽĪŖBC”–2łŲĻęĻ≤Ķ„°£
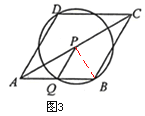
»ÁÕľ4£¨

°—PĻżĶ„C£¨īň ĪPC=PQ£¨ľī![]() =t
=t
°ŗt=![]() °£
°£
°ŗĶĪ1°‹t°‹![]() Ī£¨°—P”ŽĪŖBC”–“ĽłŲĻęĻ≤Ķ„°£
Ī£¨°—P”ŽĪŖBC”–“ĽłŲĻęĻ≤Ķ„°£
ĶĪĶ„P‘ň∂ĮĶĹĶ„C£¨ľīt=2 Ī£¨Q°ĘB÷ōļŌ£¨°—PĻżĶ„B£¨
īň Ī£¨°—P”ŽĪŖBC”–“ĽłŲĻęĻ≤Ķ„°£
◊Ř…Ōňý Ų£¨ĶĪt=![]() ĽÚ1°‹t°‹
ĽÚ1°‹t°‹![]() ĽÚt=2 Ī£¨°—P”ŽŃ‚–őABCDĶńĪŖBC”–1łŲĻęĻ≤Ķ„£ĽĶĪ
ĽÚt=2 Ī£¨°—P”ŽŃ‚–őABCDĶńĪŖBC”–1łŲĻęĻ≤Ķ„£ĽĶĪ![]() Ī£¨°—P”ŽĪŖBC”–2łŲĻęĻ≤Ķ„°£
Ī£¨°—P”ŽĪŖBC”–2łŲĻęĻ≤Ķ„°£
°ĺĹ‚őŲ°Ņ
÷ĪŌŖ”Ž‘≤ĶńőĽ÷√ĻōŌĶ£¨Ń‚–őĶń–‘÷ £¨ļ¨30°„Ĺ«÷ĪĹ«»żĹ«–őĶń–‘÷ £¨Ōŗň∆»żĹ«–őĶńŇ–∂®ļÕ–‘÷ £¨∆Ĺ––ĶńŇ–∂®£¨«–ŌŖĶń–‘÷ £¨Ķ»ĪŖ»żĹ«–őĶńŇ–∂®ļÕ–‘÷ °£
£®2£©∑÷°—P”ŽBC«–”ŕĶ„M£¨°—PĻżĶ„B£¨°—PĻżĶ„CļÕĶ„P‘ň∂ĮĶĹĶ„Cňńłų«ťŅŲŐ÷¬ŘľīŅ…°£

 ‘ń∂ŃŅž≥ĶŌĶŃ–īūįł
‘ń∂ŃŅž≥ĶŌĶŃ–īūįł