题目内容
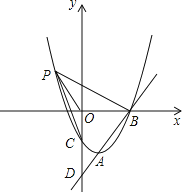
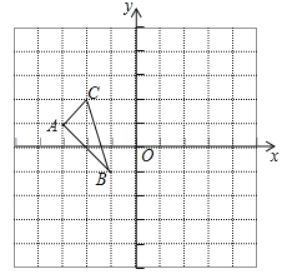
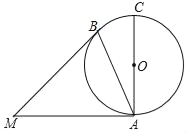
【题目】如图，在平面直角坐标系中，一个含有45角的三角板的其中一个锐角顶点置于点A（﹣3，﹣3）处，将其绕点A旋转，这个45角的两边所在的直线分别交x轴，y轴的正半轴于点B，C，连结BC，函数y＝
（x＞0）的图象经过BC的中点D，则（ ）
A. 
B. 
C. 
D. 
【答案】D
【解析】
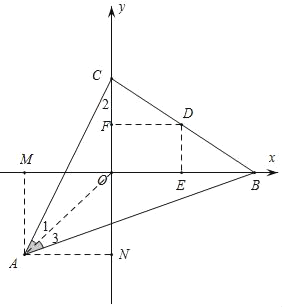
过A点作AM⊥x轴，AN⊥y轴，连接AO，根据A点坐标可知OA长度，再证明△AOC∽△BOA，根据得到的比例式计算出OBOC；过D点作DE⊥x轴，DF⊥y轴，根据D为BC中点可以计算出DEDF，从而确定了k值．
过A点作AM⊥x轴，AN⊥y轴，
则四边形AMON是正方形，连接AO．
由A（﹣3，﹣3）可得OA＝3
，
则∠AOC＝∠BOA＝135°，
∵∠1+∠2＝45°，∠1+∠3＝45°，
∴∠2＝∠3．
∴△AOC∽△BOA．
∴
，即OA2＝OBOC＝18，
∴S△OBC＝
×18＝9，
过D点作DE⊥x轴，DF⊥y轴，∵D为BC中点，∴DE＝OD，DF＝OB，
k＝DEOF＝
OBOC＝
，
故选D．
练习册系列答案
相关题目
