题目内容

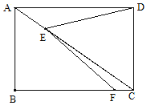
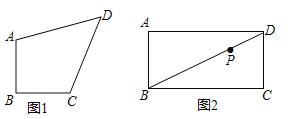
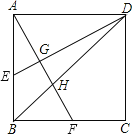
【题目】如图，已知四边形ABCD是边长为2的正方形，E是AB的中点，F是BC的中点，AF与DE相交于G，BD和AF相交于H，那么四边形BEGH的面积是（　　）

A. B. C. D.

【答案】C

【解析】

根据BC∥AD，可证△ADH∽△FBH，可以计算△ADH的面积，根据△AEG∽△DEA可以求△AEG的面积，即可解题．

∵BC∥AD，∴△BFH∽△DAH，且相似比为1：2，∴△ADH的面积为，△FBH的面积为

又∵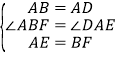，∴△ABF≌△DAE，（SAS）

∴∠BAF=∠ADE，∠BAF+∠AEG=90°，∴∠AGE=90°，∴△AEG∽△EDA，∴，解得：AG，EG，∴△AEG的面积，∴四边形BEGH的面积=△ABD的面积－△AGE的面积－△AHD的面积=2×2．

故选C．

练习册系列答案
相关题目

【题目】已知如图 1，在△ABC 中，∠ACB＝90°，BC＝AC，点 D 在 AB 上，DE⊥AB交 BC 于 E，点 F 是 AE 的中点

（1） 写出线段 FD 与线段 FC 的关系并证明；

（2） 如图 2，将△BDE 绕点 B 逆时针旋转α（0°＜α＜90°），其它条件不变，线段 FD 与线段 FC 的关系是否变化，写出你的结论并证明；

（3） 将△BDE 绕点 B 逆时针旋转一周，如果 BC＝4，BE＝2，直接写出线段 BF 的范围．

【题目】已知，数轴上三个点A、O、P，点O是原点，固定不动，点A和B可以移动，点A表示的数为，点B表示的数为.

（1）若A、B移动到如图所示位置，计算的值.

（2）在（1）的情况下，B点不动，点A向左移动3个单位长，写出A点对应的数，并计算.

（3）在（1）的情况下，点A不动，点B向右移动15.3个单位长，此时比大多少？请列式计算.

【题目】一个边长为 4cm 的等边三角形 ABC 与⊙O 等高， 如图放置，⊙O 与 BC 相切于点 C，⊙O 与 AC 相交于点E，则 CE 的长为 _____cm．

【题目】如图，矩形ABCD的对角线上有动点E，连结DE，边BC上有一定点F，连接EF，已知AB=3cm，AD=4cm，设A，E两点间的距离为xcm，D，E两点间的距离为y1cm，E，F两点间的距离为y2cm.小胜根据学习函数的经验，分别对函数y1，y2随自变量x的变化而变化的规律进行了探究.

下面是小胜的探究过程，请补充完整：

（1）按照下表中自变量x的值进行取点、画图、测量，得到x与y的几组对应值；

（2）在同一平面直角坐标系xOy中，描出补全后的表中各组数值所对应的点（x，y1），（x，y2），并画出函数y1，y2的图象；

（3）结合函数图象，解决问题：当DE＞EF时，AE的长度范围约为多少cm．

【题目】如图1，Rt△ACB 中，∠C=90°，点D在AC上，∠CBD=∠A，过A、D两点的圆的圆心O在AB上．

（1）利用直尺和圆规在图1中画出⊙O（不写作法，保留作图痕迹，并用黑色水笔把线条描清楚）；

（2）判断BD所在直线与（1）中所作的⊙O的位置关系，并证明你的结论；

（3）设⊙O交AB于点E，连接DE，过点E作EF⊥BC，F为垂足，若点D是线段AC的黄金分割点（即），如图2，试说明四边形DEFC是正方形．

【题目】将平行四边形纸片ABCD按如图方式折叠，使点C与点A重合，点D落到D’处，折痕为EF.

(1)、求证：△ABE≌△AD’F;

(2)、连接CF,判断四边形AECF是否为平行四边形？请证明你的结论。

(3)、若AE=5，求四边形AECF的周长。

【题目】定义：有一组邻边相等，并且它们的夹角是直角的凸四边形叫做等腰直角四边形．

（1）如图1，等腰直角四边形ABCD，AB=BC，∠ABC=90°．

①若AB=CD=1，AB∥CD，求对角线BD的长．

②若AC⊥BD，求证：AD=CD；

（2）如图2，在矩形ABCD中，AB=5，BC=9，点P是对角线BD上一点，且BP=2PD，过点P作直线分别交边AD，BC于点E，F，使四边形ABFE是等腰直角四边形，求AE的长．

【题目】已知开口向下的抛物线y=ax2-2ax+2与y轴的交点为A，顶点为B，对称轴与x轴的交点为C，点A与点D关于对称轴对称，直线BD与x轴交于点M，直线AB与直线OD交于点N．

(1)求点D的坐标.

(2)求点M的坐标(用含a的代数式表示).

(3)当点N在第一象限，且∠OMB=∠ONA时，求a的值．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网