题目内容
【题目】定义:如图1,点M,N把线段AB分割成AM,MN和BN,若以AM,MN,BN为边的三角形是一个直角三角形,则称点M,N是线段AB的勾股分割点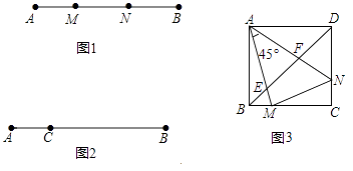
(1)已知点M,N是线段AB的勾股分割点,若AM=3,MN=4求BN的长;
(2)已知点C是线段AB上的一定点,其位置如图2所示,请在BC上画一点D,使C,D是线段AB的勾股分割点(要求尺规作图,保留作图痕迹,画出一种情形即可)
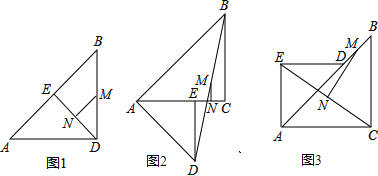
(3)如图3,正方形ABCD中,M,N分别在BC,DC上,且BM≠DN,∠MAN=45°,AM,AN分别交BD于E,F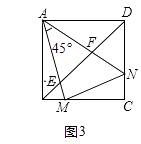
求证:①E、F是线段BD的勾股分割点;
②△AMN的面积是△AEF面积的两倍.
【答案】
(1)
解:解:(1)①当MN为最大线段时,
∵点M,N是线段AB的勾股分割点,
∴BM= ![]() =
= ![]() =
= ![]() ,
,
②当BN为最大线段时,
∵点M,N是线段AB的勾股分割点,
∴BN= ![]() =
= ![]() =5,
=5,
综上,BN= ![]() 或5;
或5;
(2)
解:作法:①在AB上截取CE=CA;
②作AE的垂直平分线,并截取CF=CA;
③连接BF,并作BF的垂直平分线,交AB于D;
点D即为所求;如图2所示.
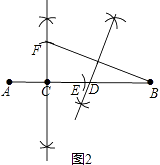
(3)
解:①如图3中,将△ADF绕点A顺时针旋转90°得到△ABH,连接HE.
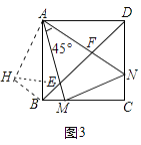
∵∠DAF+∠BAE=90°﹣∠EAF=45°,∠DAF=∠BAE,
∴∠EAH=∠EAF=45°,
∵EA=EA,AH=AD,
∴△EAH≌△EAF,
∴EF=HE,
∵∠ABH=∠ADF=45°=∠ABD,
∴∠HBE=90°,
在Rt△BHE中,HE2=BH2+BE2,
∵BH=DF,EF=HE,
∵EF2=BE2+DF2,
∴E、F是线段BD的勾股分割点.
②证明:如图4中,连接FM,EN.
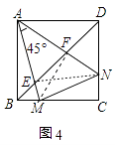
∵四边形ABCD是正方形,
∴∠ADC=90°,∠BDC=∠ADB=45°,
∵∠MAN=45°,
∴∠EAN=∠EDN,∵∠AFE=∠FDN,
∴△AFE∽△DFN,
∴∠AEF=∠DNF, ![]() =
= ![]() ,
,
∴ ![]() =
= ![]() ,∵∠AFD=∠EFN,
,∵∠AFD=∠EFN,
∴△AFD∽△EFN,
∴∠DAF=∠FEN,
∵∠DAF+∠DNF=90°,
∴∠AEF+∠FEN=90°,
∴∠AEN=90°
∴△AEN是等腰直角三角形,
同理△AFM是等腰直角三角形;
∵△AEN是等腰直角三角形,同理△AFM是等腰直角三角形,
∴AM= ![]() AF,AN=
AF,AN= ![]() AE,
AE,
∵S△AMN= ![]() AMANsin45°,
AMANsin45°,
S△AEF= ![]() AEAFsin45°,
AEAFsin45°,
∴ ![]() =
= 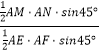 =2,
=2,
∴S△AMN=2S△AEF.
【解析】(1)①当MN为最大线段时,由勾股定理求出BN;②当BN为最大线段时,由勾股定理求出BN即可;(2)①在AB上截取CE=CA;②作AE的垂直平分线,并截取CF=CA;③连接BF,并作BF的垂直平分线,交AB于D;(3)①如图3中,将△ADF绕点A顺时针性质90°得到△ABH,连接HE,只要证明△EAH≌△EAF,推出EF=HE,再证明∠HBE=90°即可.②如图4中,连接FM,EN.首先证明△AEN是等腰直角三角形,△AFM是等腰直角三角形,推出AM= ![]() AF,AN=
AF,AN= ![]() AE,由S△AMN=
AE,由S△AMN= ![]() AMANsin45°,S△AEF=
AMANsin45°,S△AEF= ![]() AEAFsin45°,即可解决问题.
AEAFsin45°,即可解决问题.

 名校课堂系列答案
名校课堂系列答案