��Ŀ����
����Ŀ����֪����Rt��ABC�͵���Rt��AED�У���ACB=��AED=90������AD=AC��
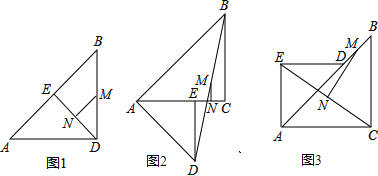
��1�����֣���ͼ1������E��AB���ҵ�C�͵�D�غ�ʱ������M��N�ֱ���DB��EC���е㣬��MN��EC��λ�ù�ϵ�� ��MN��EC��������ϵ�� ��
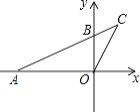
��2��̽�������ѣ�1��С���е���AED�Ƶ�A˳ʱ����ת45���õ���ͼ2������BD��EC��������DB��EC���е�M��N����MN��EC��λ�ù�ϵ��������ϵ��Ȼ�ܳ������������������֤����������������˵�����ɣ�
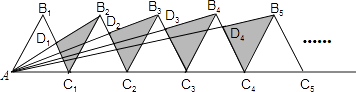
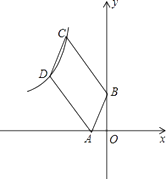
��3�����ѣ�1��С���е���AED�Ƶ�A��ʱ����ת45���õ���ͼ3������BD��EC��������DB��EC���е�M��N����MN��EC��λ�ù�ϵ��������ϵ��Ȼ�ܳ������������������֤����������������˵�����ɣ�
���𰸡���1��MN��EC��MN=![]() EC����2�����������ɼ���������3�����������ɼ�����
EC����2�����������ɼ���������3�����������ɼ�����
��������
�����������1��������λ�߶�������ϵ���ֱ�����������ʼ���ֱ�ӵó����ۣ�
��2������EM���ӳ���BC��F��֤����EDM�ա�FBM�������߶εĵ�������������⣻
��3���ӳ�ED��BC�ڵ�F������AF��MF����Ͼ��ε����ʺ͵���ֱ�����������ʣ��������ýǵĵ�������������⣮
�⣺��1��MN��EC��MN=![]() EC��
EC��
�ɵ���Rt��ABC�͵���Rt��AED�У���ACB=��AED=90����
��֪��AE=BE=EC��DE��AB��
����M��N�ֱ���DB��EC���е㣬
��MN��AB����MN=![]() BE��
BE��
��MN��EC��MN=![]() EC��
EC��
��2����ͼ2
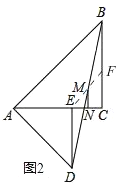
����EM���ӳ���BC��F��
�ߡ�AED=��ACB=90����
��DE��BC��
���DEM=��AFM����EDM=��MBF��
��BM=MD��
����EDM����FBM��
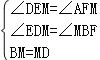 ��
��
���EDM�ա�FBM��
��BF=DE=AE��EM=FM��
��MN=![]() FC=
FC=![]() ��BC��BF��=
��BC��BF��=![]() ��AC��AF��=
��AC��AF��=![]() EC��
EC��
��MN��EC��
��3����ͼ3
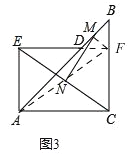
�ӳ�ED��BC�ڵ�F������AF��MF����AFΪ����ACFE�Խ��ߣ����Աؾ���EC���е�N��AN=NF=EN=NC��
��Rt��BDF�У�M��BD���е㣬��B=45����
��FD=FB��
��FM��AB��
��MN=NA=NF=NC��
��MN=![]() EC��
EC��
���NAM=��AMN����NAC=��NCA��
���MNF=��NAM+��AMN=2��NAM����FNC=��NAC+��NCA=2��NAC��
���MNC=��MNF+��FNC=2��NAM+2��NAC=2����NAM+��NAC��=2��DAC=90����
���MNC=90����
��MN��FC��MN=![]() EC��
EC��

 ��������һ���þ�ϵ�д�
��������һ���þ�ϵ�д� Сѧ��10����Ӧ����ϵ�д�
Сѧ��10����Ӧ����ϵ�д�