题目内容
【题目】如图，已知⊙O的半径为4，OA为半径，CD为弦，OA与CD交于点M，将弧CD沿着CD翻折后，点A与圆心O重合，延长OA至P，使AP=OA，连接PC.
（1）求CD的长；
（2）求证：PC是⊙O的切线.
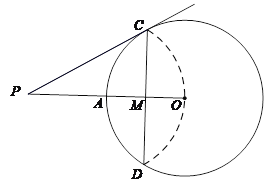
【答案】（1）4
(2) PC与☉O相切
【解析】（1）连接OC，根据翻折的性质求出OM，CD⊥OA，再利用勾股定理列式求解即可；
（2）利用勾股定理列式求出PC，然后利用勾股定理逆定理求出∠PCO=90°，再根据圆的切线的定义证明即可,
（1）连接OC，
∵弧CD沿CD翻折后，A与O重合，
∴OM=
OA=2，CD⊥OA
∵OC=4，
∴CD=2CM=2
=4；
(2)∵PA=OA=4,AM=OM=2,CM=2，PM=PA+AM=6，
又∵
CMP=∠OMC=90°
∴PC=
=4
∵OC=4,PO=8，
∴PC
+OC=PO
∴∠PCO=90°
∴PC与☉O相切
练习册系列答案
相关题目
【题目】人民网为了解百姓对时事政治关心程度，特对18～35岁的青年人每天发微博数量进行调查，设一个人的“日均发微博条数”为m，规定：当m≥10时为甲级，当5≤m＜10时为乙级，当0≤m＜5时为丙级，现随机抽取20个符合年龄条件的青年人开展调查，所抽青年人的“日均发微博条数”的数据如下：
0 | 8 | 2 | 8 | 10 | 13 | 7 | 5 | 7 | 3 |
12 | 10 | 7 | 11 | 3 | 6 | 8 | 14 | 15 | 12 |
（1）样本数据中为甲级的频率为；（直接填空）
（2）求样本中乙级数据的中位数和众数．
（3）从样本数据为丙级的人中随机抽取2人，用列举法或树状图求抽得2个人的“日均发微博条数”都是3的概率．
