题目内容
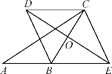
【题目】如图,OC是∠AOB内的一条射线,OD、OE分别平分∠AOB、∠AOC.
(1)若∠AOC=20°,∠AOB=110°,则∠BOC= °,∠DOE= °;
(2)若∠AOC=m°,∠AOB=n°(n>m),则∠BOC= °,∠DOE= °;
(3)猜想:∠DOE与∠BOC有怎样的数量关系?并说明理由.

【答案】(1)90,45;(2)(n﹣m),![]() (n﹣m);(3)∠DOE=
(n﹣m);(3)∠DOE=![]() ∠BOC.
∠BOC.
【解析】
(1) 依据∠AOC=20°, ∠AOB=110°, 可得∠BOC=110° -20°=90°; 再根据OD、 OE分别平分∠AOB, ∠AOC, 即可得到∠DOE的度数;
(2) 依据∠AOC= m°, ∠AOB= n°,可得∠BOC= n°- m°= (n°- m°); 再根据OD、 OE分别平分∠AOB、 ∠AOC, 可得∠AOD= ![]() n°, LAOE=
n°, LAOE= ![]() m°,进而得出∠DOE的度数;
m°,进而得出∠DOE的度数;
(3) 依据OD、 OE分别平分∠AOB、 ∠AOC, 即可得出∠AOD=![]() ∠AOB, ∠AOE=
∠AOB, ∠AOE=![]() ∠AOC, 进而得到∠DOE=∠AOD-∠AOE=
∠AOC, 进而得到∠DOE=∠AOD-∠AOE= ![]() (∠AOB-∠AOC) =
(∠AOB-∠AOC) =![]() ∠BOC.
∠BOC.
解:(1)
∵∠AOC=20°,∠AOB=110°,
∴∠BOC=110°﹣20°=90°;
∵OD、OE分别平分∠AOB、∠AOC,
∴∠AOD=55°,∠AOE=10°,
∴∠DOE=55°﹣10°=45°;
故答案为:90,45;
(2)∵∠AOC=m°,∠AOB=n°,
∴∠BOC=n°﹣m°=(n﹣m)°;
∵OD、OE分别平分∠AOB、∠AOC,
∴∠AOD=![]() n°,∠AOE=
n°,∠AOE=![]() m°,
m°,
∴∠DOE=∠AOD﹣∠AOE=![]() (n﹣m)°;
(n﹣m)°;
故答案为:(n﹣m),![]() (n﹣m);
(n﹣m);
(3)∠DOE=![]() ∠BOC.
∠BOC.
证明:∵OD、OE分别平分∠AOB、∠AOC,
∴∠AOD=![]() ∠AOB,∠AOE=∠AOC,
∠AOB,∠AOE=∠AOC,
∴∠DOE=∠AOD﹣∠AOE=![]() (∠AOB﹣∠AOC)=
(∠AOB﹣∠AOC)=![]() ∠BOC.
∠BOC.

 活力课时同步练习册系列答案
活力课时同步练习册系列答案