题目内容
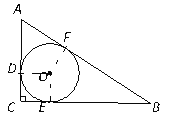
【题目】如图,⊙O是△ABC的内切圆,切点为D,E,F,若AD、BE的长为方程![]() 的两个根,则△ABC的周长为 ______.
的两个根,则△ABC的周长为 ______.

【答案】40;
【解析】求△ABC的周长,关键是求出两条直角边的长;由已知的方程可求出AF、BE的长,结合切线长定理和勾股定理,可求得CE、CF的长,进而可求出AC、BC的长;再由勾股定理求得AB,即可求△ABC的周长.
如图;
解方程![]() ,得:
,得:
x=12,x=5,
∴AD=AF=5,BF=BE=12;AB=17,
设CE=CD=x,则AC=5+x,BC=12+x;
由勾股定理,得:
AB2=AC2+BC2,即172=(5+x)2+(12+x)2,
解得:x=3(负值舍去),
∴AC=8,BC=15;
因此△ABC的周长=AC+BC+AB=8+15+17=40,.
故答案为:40.

练习册系列答案
 名校名师培优作业本加核心试卷系列答案
名校名师培优作业本加核心试卷系列答案 全程金卷系列答案
全程金卷系列答案
相关题目