题目内容
【题目】如图,在平面直角坐标系中,O为坐标原点,△ABC的边BC在y轴的正半轴上,点A在x轴的正半轴上,点C的坐标为(0,8),将△ABC沿直线AB折叠,点C落在x轴的负半轴D(﹣4,0)处.
(1)求直线AB的解析式;
(2)点P从点A出发以每秒4 ![]() 个单位长度的速度沿射线AB方向运动,过点P作PQ⊥AB,交x轴于点Q,PR∥AC交x轴于点R,设点P运动时间为t(秒),线段QR长为d,求d与t的函数关系式(不要求写出自变量t的取值范围);
个单位长度的速度沿射线AB方向运动,过点P作PQ⊥AB,交x轴于点Q,PR∥AC交x轴于点R,设点P运动时间为t(秒),线段QR长为d,求d与t的函数关系式(不要求写出自变量t的取值范围);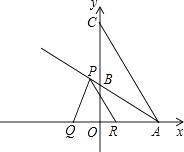
(3)在(2)的条件下,点N是射线AB上一点,以点N为圆心,同时经过R、Q两点作⊙N,⊙N交y轴于点E,F.是否存在t,使得EF=RQ?若存在,求出t的值,并求出圆心N的坐标;若不存在,说明理由.
【答案】
(1)
解:∵C(0,8),D(﹣4,0),
∴OC=8,OD=4,
设OB=a,则BC=8﹣a,
由折叠的性质可得:BD=BC=8﹣a,
在Rt△BOD中,∠BOD=90°,DB2=OB2+OD2,
则(8﹣a)2=a2+42,
解得:a=3,
则OB=3,
则B(0,3),
tan∠ODB= ![]() =
= ![]() ,
,
由折叠的性质得:∠ADB=∠ACB,
则tan∠ACB=tan∠ODB= ![]() ,
,
在Rt△AOC中,∠AOC=90°,tan∠ACB= ![]() =
= ![]() ,
,
则OA=6,
则A(6,0),
设直线AB的解析式为:y=kx+b,
则 ![]() ,
,
解得: 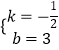 ,
,
故直线AB的解析式为:y=﹣ ![]() x+3
x+3
(2)
解:在Rt△AOB中,∠AOB=90°,OB=3,OA=6,
则AB= ![]() =3
=3 ![]() ,tan∠BAO=
,tan∠BAO= ![]() =
= ![]() ,cos∠BAO=
,cos∠BAO= ![]() =
= ![]() ,
,
在Rt△PQA中,∠APQ=90°,AP=4 ![]() t,
t,
则AQ= ![]() =10t,
=10t,
∵PR∥AC,
∴∠APR=∠CAB,
由折叠的性质得:∠BAO=∠CAB,
∴∠BAO=∠APR,
∴PR=AR,
∵∠RAP+∠PQA=∠APR+∠QPR=90°,
∴∠PQA=∠QPR,
∴RP=RQ,
∴RQ=AR,
∴QR= ![]() AQ=5t,
AQ=5t,
即d=5t;
(3)
解:过点分别作NT⊥RQ于T,NS⊥EF于S,
∵EF=QR,
∴NS=NT,
∴四边形NTOS是正方形,
则TQ=TR= ![]() QR=
QR= ![]() t,
t,
∴NT= ![]() AT=
AT= ![]() (AQ﹣TQ)=
(AQ﹣TQ)= ![]() (10t﹣
(10t﹣ ![]() t)=
t)= ![]() t,
t,
分两种情况,
若点N在第二象限,则设N(n,﹣n),
点N在直线y=﹣ ![]() x+3上,
x+3上,
则﹣n=﹣ ![]() n+3,
n+3,
解得:n=﹣6,
故N(﹣6,6),NT=6,
即 ![]() t=6,
t=6,
解得:t= ![]() ;
;
若点N在第一象限,设N(N,N),
可得:n=﹣ ![]() n+3,
n+3,
解得:n=2,
故N(2,2),NT=2,
即 ![]() t=2,
t=2,
解得:t= ![]() .
.
故当t= ![]() 或t=
或t= ![]() 时,QR=EF,N(﹣6,6)或(2,2).
时,QR=EF,N(﹣6,6)或(2,2).

【解析】(1)由C(0,8),D(﹣4,0),可求得OC,OD的长,然后设OB=a,则BC=8﹣a,在Rt△BOD中,由勾股定理可得方程:(8﹣a)2=a2+42 , 解此方程即可求得B的坐标,然后由三角函数的求得点A的坐标,再利用待定系数法求得直线AB的解析式;(2)在Rt△AOB中,由勾股定理可求得AB的长,继而求得∠BAO的正切与余弦,由PR∥AC与折叠的性质,易证得RQ=AR,则可求得d与t的函数关系式;(3)首先过点分别作NT⊥RQ于T,NS⊥EF于S,易证得四边形NTOS是正方形,然后分别从点N在第二象限与点N在第一象限去分析求解即可求得答案.

 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案