题目内容
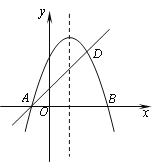
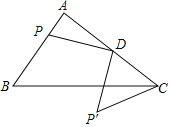
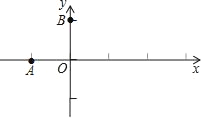
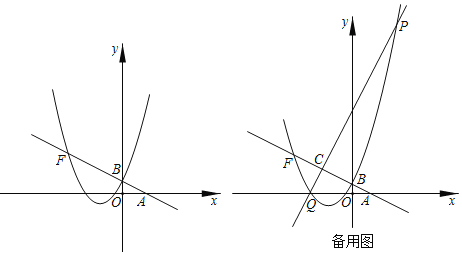
【题目】如图,直线y=﹣![]() x+1与x轴,y轴分别交于A,B两点,抛物线y=ax2+bx+c过点B,并且顶点D的坐标为(﹣2,﹣1).
x+1与x轴,y轴分别交于A,B两点,抛物线y=ax2+bx+c过点B,并且顶点D的坐标为(﹣2,﹣1).
(1)求该抛物线的解析式;
(2)若抛物线与直线AB的另一个交点为F,点C是线段BF的中点,过点C作BF的垂线交抛物线于点P,Q,求线段PQ的长度;
(3)在(2)的条件下,点M是直线AB上一点,点N是线段PQ的中点,若PQ=2MN,直接写出点M的坐标.
【答案】(1)y=![]() x2+2x+1;(2)5
x2+2x+1;(2)5![]() ;(3)M(
;(3)M(![]() ,﹣
,﹣![]() )或(﹣
)或(﹣![]() ,
,![]() )
)
【解析】
(1)先求出点B坐标,再将点D,B代入抛物线的顶点式即可;
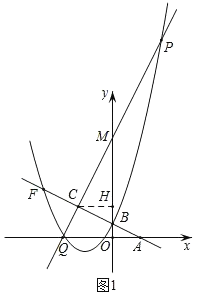
(2)如图1,过点C作CH⊥y轴于点H,先求出点F的坐标,点C的坐标,再求出直线CM的解析式,最后可求出两个交点及交点间的距离;
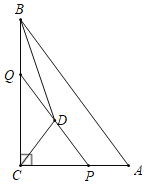
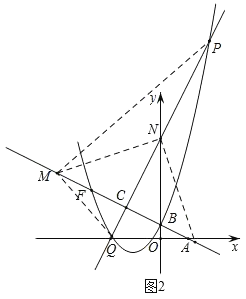
(3)设M(m,﹣![]() m+1),如图2,取PQ的中点N,连接MN,证点P,M,Q同在以PQ为直径的圆上,所以∠PMQ=90°,利用勾股定理即可求出点M的坐标.
m+1),如图2,取PQ的中点N,连接MN,证点P,M,Q同在以PQ为直径的圆上,所以∠PMQ=90°,利用勾股定理即可求出点M的坐标.
解:(1)在y=﹣![]() x+1中,
x+1中,
当x=0时,y=1,
∴B(0,1),
∵抛物线y=ax2+bx+c过点B,并且顶点D的坐标为(﹣2,﹣1),
∴可设抛物线解析式为y=a(x+2)2﹣1,
将点B(0,1)代入,
得,a=![]() ,
,
∴抛物线的解析式为:y=![]() (x+2)2﹣1=
(x+2)2﹣1=![]() x2+2x+1;
x2+2x+1;
(2)联立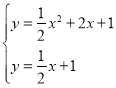 ,
,
解得,![]() 或
或 ,
,
∴F(﹣5,![]() ),
),
∵点C是BF的中点,
∴xC=![]() =﹣
=﹣![]() ,yC=
,yC=![]() =
=![]() ,
,
∴C(﹣![]() ,
,![]() ),
),
如图1,过点C作CH⊥y轴于点H,
则∠HCB+∠CBH=90°,
又∵∠MCH+∠HCB=90°,
∴∠CBH=∠MCH,
又∠CHB=∠MHC=90°,
∴△CHB∽△MHC,
∴![]() =
=![]() ,
,
即![]() =
=![]() ,
,
解得,HM=5,
∴OM=OH+MH=![]() +5=
+5=![]() ,
,
∴M(0,![]() ),
),
设直线CM的解析式为y=kx+![]() ,
,
将C(﹣![]() ,
,![]() )代入,
)代入,
得,k=2,
∴yCM=2x+![]() ,
,
联立2x+![]() =
=![]() x2+2x+1,
x2+2x+1,
解得,x1=![]() ,x2=﹣
,x2=﹣![]() ,
,
∴P(![]() ,5
,5![]() +
+![]() ),Q(﹣
),Q(﹣![]() ,﹣5
,﹣5![]() +
+![]() ),
),
∴PQ=![]() =5
=5![]() ;
;
(3)∵点M在直线AB上,
∴设M(m,﹣![]() m+1),
m+1),
如图2,取PQ的中点N,连接MN,
∵PQ=2MN,
∴NM=NP=NQ,
∴点P,M,Q同在以PQ为直径的圆上,
∴∠PMQ=90°,
∴MP2+MQ2=PQ2,
∴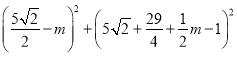 +
+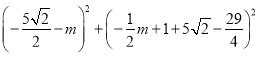 =(5
=(5![]() )2,
)2,
解得,m1=![]() ,m2=﹣
,m2=﹣![]() ,
,
∴M(![]() ,﹣
,﹣![]() )或(﹣
)或(﹣![]() ,
,![]() ).
).

 名校课堂系列答案
名校课堂系列答案