题目内容
【题目】如图，在Rt△ABC中，∠C＝90°，点P是边AC上一点，过点P作PQ∥AB交BC于点Q，D为线段PQ的中点，BD平分∠ABC，以下四个结论①△BQD是等腰三角形；②BQ＝DP；③PA＝
QP；④
＝（1+
）2；其中正确的结论的个数（ ）
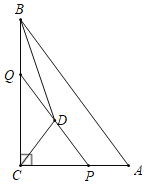
A.1个B.2个C.3个D.4个
【答案】C
【解析】
利用平行线的性质角、平分线的定义、相似三角形的判定和性质一一判断即可．
解：∵PQ∥AB，
∴∠ABD＝∠BDQ，又∠ABD＝∠QBD，
∴∠QBD＝∠BDQ，
∴QB＝QD，
∴△BQD是等腰三角形，故①正确，
∵QD＝DF，
∴BQ＝PD，故②正确，
∵PQ∥AB，
∴
＝
，
∵AC与BC不相等，
∴BQ与PA不一定相等，故③错误，
∵∠PCQ＝90°，QD＝PD，
∴CD＝QD＝DP，
∵△ABC∽△PQC，
∴
＝（
）2＝（
）2＝（1+
）2，故④正确，
故选：C．
练习册系列答案
相关题目
