题目内容
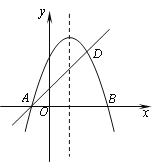
【题目】如图，抛物线y=-x2＋bx＋c与x轴交于A、B两点，且B点的坐标为（3，0），经过A点的直线交抛物线于点D （2， 3）.
（1）求抛物线的解析式和直线AD的解析式；
（2）过x轴上的点E （a，0） 作直线EF∥AD，交抛物线于点F，是否存在实数a，使得以A、D、E、F为顶点的四边形是平行四边形？如果存在，求出满足条件的a；如果不存在，请说明理由.
【答案】（1） y=-x2+2x+3；y=x+1；（2） a的值为-3或4±
．
【解析】
试题分析：（1）把点B和D的坐标代入抛物线y=-x2+bx+c得出方程组，解方程组即可；由抛物线解析式求出点A的坐标，设直线AD的解析式为y=kx+a，把A和D的坐标代入得出方程组，解方程组即可；
（2）分两种情况：①当a＜-1时，DF∥AE且DF=AE，得出F（0，3），由AE=-1-a=2，求出a的值；
②当a＞-1时，显然F应在x轴下方，EF∥AD且EF=AD，设F （a-3，-3），代入抛物线解析式，即可得出结果．
试题解析：（1）把点B和D的坐标代入抛物线y=-x2+bx+c得：
，
解得：b=2，c=3，
∴抛物线的解析式为y=-x2+2x+3；
当y=0时，-x2+2x+3=0，
解得：x=3，或x=-1，
∵B（3，0），
∴A（-1，0）；
设直线AD的解析式为y=kx+a，
把A和D的坐标代入得：
，
解得：k=1，a=1，
∴直线AD的解析式为y=x+1；
（2）分两种情况：①当a＜-1时，DF∥AE且DF=AE，
则F点即为（0，3），
∵AE=-1-a=2，
∴a=-3；
②当a＞-1时，显然F应在x轴下方，EF∥AD且EF=AD，
设F （a-3，-3），
由-（a-3）2+2（a-3）+3=-3，
解得：a=4±；
综上所述，满足条件的a的值为-3或4±．
