题目内容
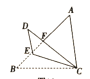
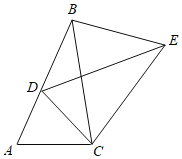
【题目】如图,将△ABC绕点C顺时针旋转得到△DEC,使点A的对应点D恰好落在边AB上,点B的对应点为E,连接BE.
(Ⅰ)求证:∠A=∠EBC;
(Ⅱ)若已知旋转角为50°,∠ACE=130°,求∠CED和∠BDE的度数.
【答案】(Ⅰ)证明见解析;(Ⅱ)∠BDE=50°, ∠CED =35°
【解析】
(Ⅰ)由旋转的性质可得AC=CD,CB=CE,∠ACD=∠BCE,由等腰三角形的性质可求解.
(Ⅱ)由旋转的性质可得AC=CD,∠ABC=∠DEC,∠ACD=∠BCE=50°,∠EDC=∠A,由三角形内角和定理和等腰三角形的性质可求解.
证明:(Ⅰ)∵将△ABC绕点C顺时针旋转得到△DEC,
∴AC=CD,CB=CE,∠ACD=∠BCE,
∴∠A=![]() ,∠CBE=
,∠CBE=![]() ,
,
∴∠A=∠EBC;
(Ⅱ)∵将△ABC绕点C顺时针旋转得到△DEC,
∴AC=CD,∠ABC=∠DEC,∠ACD=∠BCE=50°,∠EDC=∠A,∠ACB=∠DCE
∴∠A=∠ADC=65°,
∵∠ACE=130°,∠ACD=∠BCE=50°,
∴∠ACB=∠DCE =80°,
∴∠ABC=180°﹣∠BAC﹣∠BCA=35°,
∵∠EDC=∠A=65°,
∴∠BDE=180°﹣∠ADC﹣∠CDE=50°.∠CED=180°﹣∠DCE﹣∠CDE=35°

练习册系列答案
相关题目