��Ŀ����
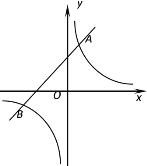
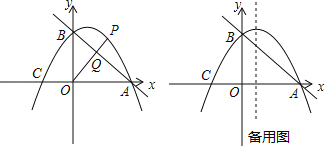
����Ŀ����ͼ��ֱ��y=��![]() x+3��x�ύ�ڵ�A����y�ύ�ڵ�B��������y=��
x+3��x�ύ�ڵ�A����y�ύ�ڵ�B��������y=��![]() x2+bx+c����A��B���㣬��x�����һ������ΪC��
x2+bx+c����A��B���㣬��x�����һ������ΪC��
��1���������ߵĽ���ʽ��
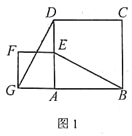
��2����P�ǵ�һ�����������ϵĵ㣬����OP��ֱ��AB�ڵ�Q�����P�ĺ�����Ϊm��PQ��OQ�ı�ֵΪy����y��m�Ĺ�ϵʽ�������PQ��OQ�ı�ֵ�����ֵ��
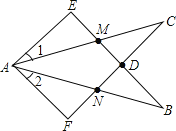
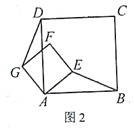
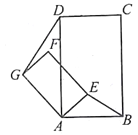
��3����D�������߶Գ����ϵ�һ���㣬����OD��CD������ODC���Բ��Բ��ΪM����sin��ODC��ֵ���ʱ�����M�����꣮
���𰸡���1�������߽���ʽΪy=��![]() x2+
x2+![]() x+3����2��y=��
x+3����2��y=��![]() m2+
m2+![]() m��PQ��OQ�ı�ֵ�����ֵΪ
m��PQ��OQ�ı�ֵ�����ֵΪ![]() ����3����M������Ϊ����1��
����3����M����������1��![]() ����1����
����1����![]() ����
����
��������
��1������ֱ�߽���ʽ��õ�A��B�����꣬�������������������߽���ʽ���ɵã�
��2������P��y���ƽ���߽�AB�ڵ�E���ݴ�֪��PEQ�ס�OBQ�����ݶ�Ӧ�߳ɱ�����y=![]() PE����P��m����
PE����P��m����![]() m2+
m2+![]() m+3����E��m����
m+3����E��m����![]() m+3����PE=��
m+3����PE=��![]() m2+
m2+![]() m�����y=
m�����y=![]() PE�ɵú�������ʽ�����ö��κ������ʵ������ֵ��
PE�ɵú�������ʽ�����ö��κ������ʵ������ֵ��
��3����CO�Ĵ�ֱƽ������CO���ڵ�N��֪��M��CO�Ĵ�ֱƽ�����ϣ�����OM��CM��DM�����ݡ�ODC=![]() ��CMO=��OMN��MC=MO=MD֪sin��ODC=sin��OMN=
��CMO=��OMN��MC=MO=MD֪sin��ODC=sin��OMN=![]() ����MDȡ��Сֵʱ��sin��ODC��ݴ˽�һ�����ɵã�
����MDȡ��Сֵʱ��sin��ODC��ݴ˽�һ�����ɵã�
��1����y=��![]() x+3����y=0��x=4����x=0��y=3��
x+3����y=0��x=4����x=0��y=3��
���A��4��0����B��0��3����
��A��4��0����B��0��3������y=��![]() x2+bx+c���ã�
x2+bx+c���ã�
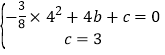 ��
��
��ã�![]() ��
��
�������߽���ʽΪy=��![]() x2+
x2+![]() x+3��
x+3��
��2����ͼ1������P��y���ƽ���߽�AB�ڵ�E��
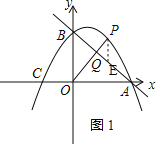
����PEQ�ס�OBQ��
��![]() ��
��
��![]() =y��OB=3��
=y��OB=3��
��y=![]() PE��
PE��
��P��m����![]() m2+
m2+![]() m+3����E��m����
m+3����E��m����![]() m+3����
m+3����
��PE=����![]() m2+
m2+![]() m+3��������
m+3��������![]() m+3��=��
m+3��=��![]() m2+
m2+![]() m��
m��
��y=![]() ����
����![]() m2+
m2+![]() m��=��
m��=��![]() m2+
m2+![]() m=��
m=��![]() ��m��2��2+
��m��2��2+![]() ��
��
��0��m��3��
�൱m=2ʱ��y���ֵ=![]() ��
��
��PQ��OQ�ı�ֵ�����ֵΪ![]() ��
��
��3����ͼ����������y=��![]() x2+
x2+![]() x+3����C����2��0�����Գ���Ϊֱ��x=1��
x+3����C����2��0�����Գ���Ϊֱ��x=1��
�ߡ�ODC������Ϊ��M��
���M��CO�Ĵ�ֱƽ�����ϣ�
��CO�Ĵ�ֱƽ������CO���ڵ�N������OM��CM��DM��
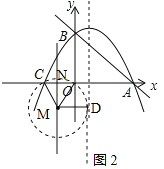
���ODC=![]() ��CMO=��OMN��MC=MO=MD��
��CMO=��OMN��MC=MO=MD��
��sin��ODC=sin��OMN=![]() ��
��
��MO=MD��
�൱MDȡ��Сֵʱ��sin��ODC���
��ʱ��M��ֱ��x=1���У�MD=2��
MN=![]() =
=![]() ��
��
���M����1����![]() ����
����
���ݶԳ��ԣ���һ�㣨��1��![]() ��Ҳ�������⣻
��Ҳ�������⣻
������������M����������1��![]() ����1����
����1����![]() ����
����