题目内容
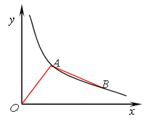
【题目】如图,双曲线y=![]() (x>0)经过A、B两点,若点A的横坐标为1,∠OAB=90°,且OA=AB,则k的值为________.
(x>0)经过A、B两点,若点A的横坐标为1,∠OAB=90°,且OA=AB,则k的值为________.
【答案】![]() .
.
【解析】分析:设A(1,n),作AE⊥x轴于E,BF⊥x轴于F,过B点作BC⊥y轴于C,交AE于G,则AG⊥BC,先求得△AOE≌△BAG,得出AG=OE=1,BG=AE=n,从而求得B(n+1,n-1),根据k=n×1=(1+n)(n-1)得出方程,解方程即可.
详解:设A(1,n),作AE⊥x轴于E,BF⊥x轴于F,过B点作BC⊥y轴于C,交AE于G,如图所示:
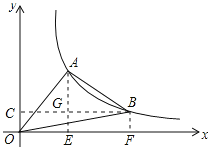
则AG⊥BC,
∵∠OAB=90°,
∴∠OAE+∠BAG=90°,
∵∠OAE+∠AOE=90°,
∴∠AOE=∠GAB,
在△AOE和△BAG中,
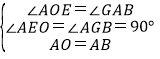 ,
,
∴△AOE≌△BAG(AAS),
∴OE=AG,AE=BG,
∵点A(1,n),
∴AG=OE=1,BG=AE=n,
∴B(1+n,n-1),
∴k=n×1=(1+n)(n-1),
整理得:n2-n-1=0,
解得:n=![]() (负值舍去),
(负值舍去),
∴n=![]() ,
,
∴k=![]() ;
;
故答案为:![]() .
.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目





