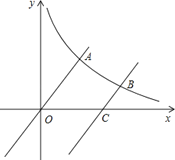
题目内容
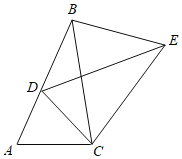
【题目】如图，在
中，
，
，
，
．则
的长为__________；若
是边上一点，将
沿
所在直线翻折得到
，
交于
，则当
时，
的值为__________．
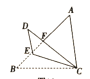
【答案】7 
【解析】
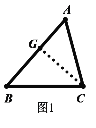
（1）如图1（见解析），过点C作
于点G，先根据等腰直角三角形的判定与性质求出
的长，再根据勾股定理求出
的长，然后根据线段的和差即可得；
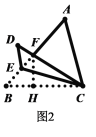
（2）如图2（见解析），过点F作
于点H，先根据折叠的性质、平行线的性质得出
，再根据相似三角形的判定与性质得出AF的长，从而可得BF的长，然后根据等腰直角三角形的判定与性质得出BH、FH的长，从而可得CH的长，最后根据正切的定义即可得．
（1）如图1，过点C作于点G
是等腰直角三角形
在
中，
故答案为：7；
（2）由折叠的性质得：
在
和
中，
，即
解得
如图2，过点F作于点H
是等腰直角三角形
则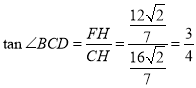
故答案为：．
练习册系列答案
相关题目
【题目】小明根据学习函数的经验，对函数
的图象与性质进行了探究．
下面是小明的探究过程，请补充完整：
（1）函数的自变量
的取值范围是__________．
（2）下表列出了
与的几组对应值，请写出
，
的值：
________，
________．
| … |
|
|
|
|
|
|
| 1 | 2 | 3 | 4 | … |
| … |
|
|
|
|
|
|
| 2 |
|
|
| … |
（3）如图，在平面直角坐标系
中，描出了以上表中各对对应值为坐标的点．根据描出的点，画出该函数的图象．
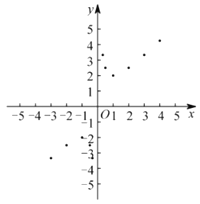
（4）结合函数的图象，请完成：
①当
时，
________；
②写出该函数的一条性质______________________________；
③若方程
有两个相等的实数根，则
的值是____________．
