Question

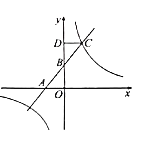
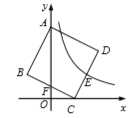
【题目】如图，正方形的顶点分别在轴和轴上，边的中点在轴上，若反比例函数的图象恰好经过的中点，则的长为__________．

Answer 1

【答案】

【解析】

过点E作EG⊥x轴于G，设点E的坐标为（），根据正方形的性质和“一线三等角”证出△CEG≌△FCO，可得EG=CO=，CG=FO=OG－OC=，然后利用等角的余角相等，可得∠BAF=∠FCO，先求出tan∠BAF，即可求出tan∠FCO，即可求出x的值，从而求出OF和OC，根据勾股定理和正方形的性质即可求出CF、BF、AB、AF，从而求出OA.

解：过点E作EG⊥x轴于G，如下图所示

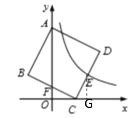
∵反比例函数的图象过点，设点E的坐标为（）

∴OG=x，EG=

∵四边形ABCD是正方形，

∴AB=BC=CD，∠ABC=∠BCD=90°

∵点E、F分别是CD、BC的中点

∴EC=CD=BC=CF

∵∠CEG＋∠ECG=90°，∠FCO＋∠ECG=90°，

∴∠CEG=∠FCO

在△CEG和△FCO中

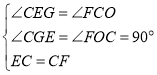
∴△CEG≌△FCO

∴EG=CO=，CG=FO=OG－OC=

∵∠BAF＋∠AFB=90°，∠FCO＋∠COF=90°，∠AFB=∠COF

∴∠BAF=∠FCO

在Rt△BAF中，tan∠BAF=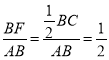

∴tan∠FCO=tan∠BAF=

在Rt△FCO中，tan∠FCO=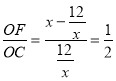

解得：

则OF==，OC=

根据勾股定理可得：CF=

∴BF=CF=，AB=BC=2 CF=，

根据勾股定理可得：AF=

∴OA=OF＋AF=

故答案为：.