题目内容
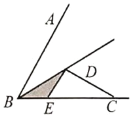
【题目】在△ABC中,∠CAB=2∠B,AE平分∠CAB,CD⊥AB于D,AC=3,AD=1.下列结论:①∠AEC=∠CAB;②EF=CE;③AC=AE;④BD=4;

正确的是___________(填序号)
【答案】①②.
【解析】
根据角平分线,三角形的外角性质以及等角对等边的性质可得出结论①②正确.
解:∵AE平分∠CAB,
∴∠CAB=2∠EAB,
∵∠CAB=2∠B,
∴∠EAB=∠B,
∵∠AEC=∠B+∠EAB,
∴∠AEC=2∠B=∠CAB,①正确;
∵CD⊥AB于D,
∴∠B+∠DCB=90°,∠EAB+∠AFD=90°,
∵∠EAB=∠B,
∴∠DCB=∠AFD,
∵∠CFE=∠AFD,
∴∠CFE=∠DCB,
∴EF=CE,②正确;
无法证明AC=AE,故③不正确;
∵AC=3,AD=1,CD⊥AB于D,
∴CD=![]() ,
,
不能得出BD=4,故④不正确.
故答案为:①②.

练习册系列答案
 津桥教育暑假拔高衔接广东人民出版社系列答案
津桥教育暑假拔高衔接广东人民出版社系列答案 波波熊暑假作业江西人民出版社系列答案
波波熊暑假作业江西人民出版社系列答案 学而优暑期衔接南京大学出版社系列答案
学而优暑期衔接南京大学出版社系列答案
相关题目