Question

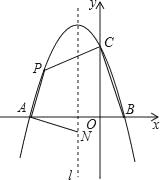
【题目】在平面直角坐标系中，抛物线经过点，且与轴的一个交点为．

（1）求抛物线的表达式；

（2）是抛物线与轴的另一个交点，点的坐标为，其中，△的面积为．

①求的值；

②将抛物线向上平移个单位，得到抛物线．若当时，抛物线与轴只有一个公共点，结合函数的图象，求的取值范围．

Answer 1

【答案】（1）；（2）①；②答案见解析.

【解析】试题分析：（1）将A、B的坐标代入抛物线解析式求出b、c即可；（2）①过A作AF⊥x轴与点F，如图1，首先求出D的坐标，再根据△ADE的面积可求出DE的长度，接着可求出OE的长度即m的值；②利用抛物线的平移变换，可设抛物线C2的表达式为y=（x－1）2－4+n，接下去分类讨论：求出抛物线过点E和过原点时对应的n的值，并画出图像，利用图像可确定n的范围；当抛物线顶点再x轴上时，求出n的值.综上得到n的取值范围.

试题解析：

（1）∵抛物线C1：y=x2+bx+c经过点A（2，－3），且与x轴的一个交点为B（3，0），

∴，

解得，

∴抛物线C1解析式为y=x2－2x－3；

（2）

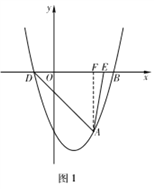
①过A作AF⊥x轴与点F，如图1，

∵y=x2－2x－3=（x－1）2－4，

∴抛物线对称轴为：x=1，

∴D（－1，0），

∵E（m，0），m＞0，

∴S△ADE=DE·AF=DE×3=，

∴DE=，

∴m=OE=DE－OD=.

②

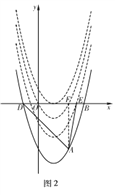
设抛物线C2的表达式为y=（x－1）2－4+n，

如图2，当抛物线C2经过E（，0）时，

（－1）2－4+n=0，解得n=；

当抛物线C2经过原点时，

（0－1）2－4+n=0，解得n=3；

∵0≤x≤时，抛物线C2与x轴只有一个公共点，

∴结合图像可知，当≤n＜3时，符合题意.

令y=0，（x－1）2－4+n=0，

由题意得，b2－4ac=16－4n=0，解得n=4.

综上， ≤n＜3或n=4.