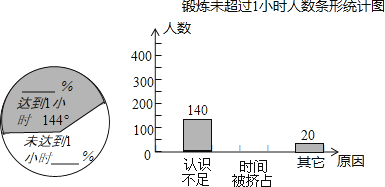
题目内容
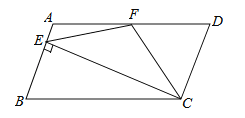
【题目】如图,在□ABCD中,AD=2AB,F是AD的中点,作CE⊥AB,垂足E在线段AB上(E不与A、B重合),连接EF、CF,则下列结论中一定成立的是 ( )
①∠DCF=![]() ∠BCD;②EF=CF;③
∠BCD;②EF=CF;③![]() ;④∠DFE=4∠AEF.
;④∠DFE=4∠AEF.
A. ①②③④ B. ①②③ C. ①② D. ①②④
【答案】B
【解析】分析:分别利用平行四边形的性质以及全等三角形的判定与性质得出△AEF≌△DMF(ASA),得出对应线段之间关系进而得出答案.
详解:①∵F是AD的中点,∴AF=FD.
∵在ABCD中,AD=2AB,∴AF=FD=CD,∴∠DFC=∠DCF.
∵AD∥BC,∴∠DFC=∠FCB,∴∠DCF=∠BCF,∴∠DCF=![]() ∠BCD,故①正确;
∠BCD,故①正确;
延长EF,交CD延长线于M.
∵四边形ABCD是平行四边形,∴AB∥CD,∴∠A=∠MDF.
∵F为AD中点,∴AF=FD.在△AEF和△DFM中, 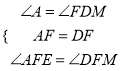 ,∴△AEF≌△DMF(ASA),∴FE=MF,∠AEF=∠M.
,∴△AEF≌△DMF(ASA),∴FE=MF,∠AEF=∠M.
∵CE⊥AB,∴∠AEC=90°,∴∠AEC=∠ECD=90°.
∵FM=EF,∴EF=CF,故②正确;
③∵EF=FM,∴S△EFC=S△CFM.
∵MC>BE,∴S△BEC<2S△EFC
故③正确;
④设∠FEC=x,则∠FCE=x,∴∠DCF=∠DFC=90°﹣x,∴∠EFC=180°﹣2x,∴∠EFD=90°﹣x+180°﹣2x=270°﹣3x.
∵∠AEF=90°﹣x,∴∠DFE=3∠AEF,故④错误.
故答案为:①②③.


练习册系列答案
相关题目