题目内容
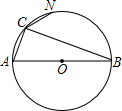
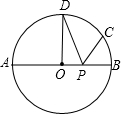
已知:如图,BC为半圆的直径,O为圆心,D是弧AC的中点,四边形ABCD的对角线AC、BD交于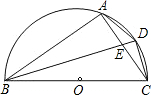 点E.
点E.
(1)求证:△ABE∽△DBC;
(2)已知BC=
,CD=
,求sin∠AEB的值;
(3)在(2)的条件下,求弦AB的长.
 点E.
点E.(1)求证:△ABE∽△DBC;
(2)已知BC=
| 5 |
| 2 |
| ||
| 2 |
(3)在(2)的条件下,求弦AB的长.
(1)证明:∵BC为半圆的直径,
∴∠BAE=∠BDC=90°.
∵D是弧AC的中点,
∴∠ABE=∠DBC.
∴△ABE∽△DBC.
(2)在RT△DCB中,
∵∠BDC=90°,BC=
,CD=
,
∴BD=
.
∴sin∠DCB=BD:BC=
.
∵△ABE∽△DBC,
∴∠AEB=∠DCB.
∴sin∠AEB=
.
(3)∵∠AEB=∠DEC,
∴sin∠DEC=
.
∴EC=1.25,DE=
,BD=
.
BE=BD-DE=
,AB=
×sin∠AEB=1.5.
∴∠BAE=∠BDC=90°.
∵D是弧AC的中点,
∴∠ABE=∠DBC.
∴△ABE∽△DBC.
(2)在RT△DCB中,
∵∠BDC=90°,BC=
| 5 |
| 2 |
| ||
| 2 |
∴BD=
| 5 |
∴sin∠DCB=BD:BC=
2
| ||
| 5 |
∵△ABE∽△DBC,
∴∠AEB=∠DCB.
∴sin∠AEB=
2
| ||
| 5 |
(3)∵∠AEB=∠DEC,
∴sin∠DEC=
2
| ||
| 5 |
∴EC=1.25,DE=
| ||
| 4 |
| 5 |
BE=BD-DE=
3
| ||
| 4 |
3
| ||
| 4 |

练习册系列答案
相关题目