题目内容
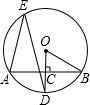
如图，AB和CD是⊙O的两条直径，弦DE∥AB，弧DE为50°的弧，那么∠BOC为（ ）
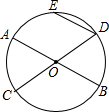
| A．115° | B．100° | C．80° | D．50° |
连接OE，
∵弧DE为50°，
∴∠EOD=50°，
∴∠OED+∠ODE=130°
∵OE=OD，
∴∠OED=∠ODE=65°，
∵DE∥AB，
∴∠AOE=∠OED=65°，
∴∠AOD=∠AOE+∠EOD=65°+50°=115°，
∴∠BOC=∠AOD=115°．
故选A．
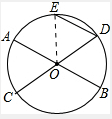
∵弧DE为50°，
∴∠EOD=50°，
∴∠OED+∠ODE=130°
∵OE=OD，
∴∠OED=∠ODE=65°，
∵DE∥AB，
∴∠AOE=∠OED=65°，
∴∠AOD=∠AOE+∠EOD=65°+50°=115°，
∴∠BOC=∠AOD=115°．
故选A．
练习册系列答案
天天向上一本好卷系列答案
小学生10分钟应用题系列答案
相关题目
点E．