题目内容
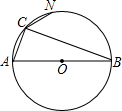
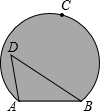
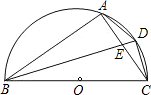
如图，AB是⊙O的直径，点N是半圆的中点，点C为
上一点，NC=
，求BC-AC的值．
 |
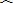| AN |
| 3 |
过N作NM⊥CN交CB于M，连接NA和NB，
∵点N是半圆的中点，
∴∠NCB=45°，
∴NC=NM，
∵AB是⊙O的直径，
∴∠ANB=∠ACB=90°，
∵∠BAN=∠BCN=45°，
∴NA=NB，∠NMB=∠NCA=135°，∠NBC=∠NAC，
∴∠MNB=∠CNA，
在△ACN和△BMN中，
，
∴△ACN≌△BMN（SAS），
∴MB=CA，
∴CB-CA=CB-MB=CM=
CN=
×
=
．
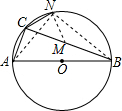
∵点N是半圆的中点，
∴∠NCB=45°，
∴NC=NM，
∵AB是⊙O的直径，
∴∠ANB=∠ACB=90°，
∵∠BAN=∠BCN=45°，
∴NA=NB，∠NMB=∠NCA=135°，∠NBC=∠NAC，
∴∠MNB=∠CNA，
在△ACN和△BMN中，
|
∴△ACN≌△BMN（SAS），
∴MB=CA，
∴CB-CA=CB-MB=CM=
| 2 |
| 2 |
| 3 |
| 6 |
练习册系列答案
名校课堂系列答案
相关题目
点E．