��Ŀ����
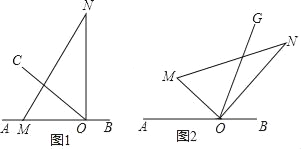
����Ŀ����ͼ1����O��ֱ��AB�ϣ���AOC��30�㣬��һֱ�����ǰ��ֱ�DZ�OM��OA�غϣ�ON�ڡ�COB�ڲ����ֽ����ǰ���O��˳ʱ�뷽����ÿ��2����ٶ���ת����ON��OB�غ�ʱֹͣת�������˶�ʱ��Ϊt(s)��
(1)��ֱ�DZ�ON����COB�ֳɡ�CON����BON��3��2����t��ֵ��
(2)��ͼ2��OGΪ���ǰ�MON�ڲ������ߣ�����ת�Ĺ����У�OGʼ��ƽ�֡�MOB�����ʡ�AOM���NOG�Ƿ����һ����������ϵ�������ڣ������������ϵ���������ڣ���˵�����ɣ�
���𰸡�(1)15��(2)��AOM��2��NOG�����ɼ�����.
��������
(1)���ݲ��ǵĶ���ɵá�COB=150�㣬���ݽ�ƽ���ߵĶ���ɵá�CON=100�㣬���ԡ�AOM=30�㣬�ݴ˼������t��ֵ��
(2)���NOGΪ������AOMΪ������MOG=90�㩁�������ݡ�AOM+��MOG+��BOG=180�㼴�ɵõ���AOM���NOG�����������ϵ��
(1)��������á�COB=180�㩁��AOC=180�㩁30��=150�㣬
�൱��CON=![]() ��COB=100��ʱ��ֱ�DZ�ON����COB�ֳɡ�CON����BON=3��2��
��COB=100��ʱ��ֱ�DZ�ON����COB�ֳɡ�CON����BON=3��2��
���AOM=30�㣬
��2t=30��
���t=15��
(2)��AOM=2��NOG��
���NOGΪ������AOMΪ������MOG=90�㩁����
�ߡ�AOM+��MOG+��BOG=180�㣬
����+90�㩁��+90�㩁��=180�㣬
������2��=0������=2����
���AOM=2��NOG��

 ���ɿ��õ�Ԫ����AB��ϵ�д�
���ɿ��õ�Ԫ����AB��ϵ�д� С�����ϵ�д�
С�����ϵ�д�