题目内容
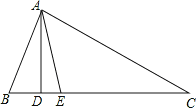
【题目】如图,在直角三角形ABC中,∠C=90°,∠CAB的平分线ADD交BC于点D,若DE垂直平分AB,则下列结论中错误的是( )
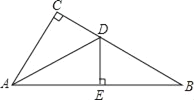
A. AB=2AE B. AC=2CD C. DB=2CD D. AD=2DE
【答案】B
【解析】
根据线段的垂直平分线的性质,等腰三角形的性质,角平分线的性质求出求出∠CAD=∠BAD=∠B=30°,根据30°角的直角三角形的性质即可判断.
解:∵DE垂直平分AB,
∴AD=BD,AB=2AE,
∴∠DAB=∠B,
∵∠CAD=∠DAB=![]() ∠BAC,
∠BAC,
∴∠BAC=2∠B,
∵∠C=90°,
∴∠B=30°,∠BAC=60°,
∴∠CAD=∠DAB=30°,
∴AD=2CD,BD=AD=2DE,
∵AD是∠CAB的平分线,DC⊥AC,DE⊥AB,
∴DE=CD,
∴BD=2CD,
∵AD=2CD,AD>AC,
∴AC≠2CD,
故选:B.

练习册系列答案
相关题目
【题目】本学期学校开展以“感受中华传统美德”为主题的研学活动,组织150名学生参观历史博物馆和民俗展览馆,每一名学生只能参加其中一项活动,共支付票款2000元,票价信息如下:
地点 | 票价 |
历史博物馆 | 10元/人 |
民俗展览馆 | 20元/人 |
(1)请问参观历史博物馆和民俗展览馆的人数各是多少人?
(2)若学生都去参观历史博物馆,则能节省票款多少元?