题目内容
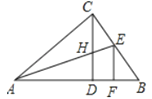
【题目】长江汛期即将来临，防汛指挥部在一危险地带两岸各安置了一探照灯，便于夜间查看江水及两岸河堤的情况．如图，灯A射线自AM顺时针旋转至AN便立即回转，灯B射线自BP顺时针旋转至BQ便立即回转，两灯不停交叉照射巡视．若灯A转动的速度是a°/秒，灯B转动的速度是b°/秒，且a、b满足|a﹣3b|+（a+b﹣4）2=0．假定这一带长江两岸河堤是平行的，即PQ∥MN，且∠BAN=45°
（1）求a、b的值；
（2）若灯B射线先转动20秒，灯A射线才开始转动，在灯B射线到达BQ之前，A灯转动几秒，两灯的光束互相平行？
（3）如图，两灯同时转动，在灯A射线到达AN之前．若射出的光束交于点C，过C作CD⊥AC交PQ于点D，则在转动过程中，
= 。
【答案】（1）a=3，b=1；
（2）当t=10秒或85秒时，两灯的光束互相平行；
（3）∠BAC：∠BCD=3：2
【解析】分析：
（1）根据|a-3b|+
=0，可得a-3b=0，且a+b-4=0，进而得出a、b的值；
（2）设A灯转动x秒，两灯的光束互相平行，分两种情况进行讨论：①在灯A射线转到AN之前，②在灯A射线转到AN之后，分别求得t的值即可；
（3）设灯A射线转动时间为t秒，根据∠BAC=45°-（180°-3t）=3t-135°，∠BCD=90°-∠BCA=90°-（180°-2t）=2t-90°，可得∠BAC与∠BCD的数量关系．
本题解析：（1）∵a、b满足|a﹣3b|+（a+b﹣4）2=0，
∴a﹣3b=0，且a+b﹣4=0，
∴a=3，b=1；
（2）设A灯转动x秒，两灯的光束互相平行，
①在灯A射线转到AN之前，
3t=（20+t）×1 解得t=10；
②在灯A射线转到AN之后，
3t﹣3×60+（20+t）×1=180， 解得t=85
综上所述，当t=10秒或85秒时，两灯的光束互相平行；
（3）(3)设灯A射线转动时间为t秒，
∵∠CAN=
3t，
∴∠BAC=
(3t)=3t
，
又∵PQ∥MN，
∴∠BCA=∠CBD+∠CAN=t+3t=2t，
而∠ACD=
，
∴∠BCD=∠BCA=(2t)=2t，
∴
，
