题目内容
如图，在直角坐标系中，矩形OABC的顶点O与坐标原点重合，A、C分别在坐标轴上，点B的坐标为（4，2），直线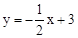
交AB，BC分别于点M，N，反比例函数
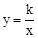的图象经过点M，N．
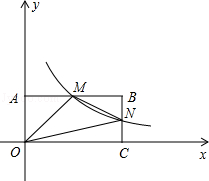
（1）求反比例函数的解析式；
（2）若点P在y轴上，且△OPM的面积与四边形BMON的面积相等，求点P的坐标．
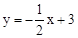交AB，BC分别于点M，N，反比例函数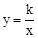的图象经过点M，N．（1）求反比例函数的解析式；
（2）若点P在y轴上，且△OPM的面积与四边形BMON的面积相等，求点P的坐标．
解：（1）∵B（4，2），四边形OABC是矩形，∴OA=BC=2。
将y=2代入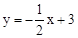3得：x=2，∴M（2，2）。
把M的坐标代入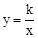得：k=4，
∴反比例函数的解析式是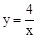
（2）
。
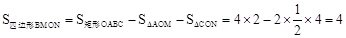∵△OPM的面积与四边形BMON的面积相等，∴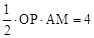
。
∵AM=2，∴OP=4。
∴点P的坐标是（0，4）或（0，－4）。
将y=2代入
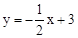3得：x=2，∴M（2，2）。把M的坐标代入
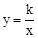得：k=4，∴反比例函数的解析式是
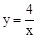
（2）
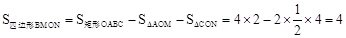。∵△OPM的面积与四边形BMON的面积相等，∴
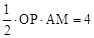。∵AM=2，∴OP=4。
∴点P的坐标是（0，4）或（0，－4）。
（1）求出OA=BC=2，将y=2代入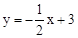求出x=2，得出M的坐标，把M的坐标代入反比例函数的解析式即可求出答案。
（2）求出四边形BMON的面积，求出OP的值，即可求出P的坐标。
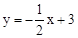求出x=2，得出M的坐标，把M的坐标代入反比例函数的解析式即可求出答案。（2）求出四边形BMON的面积，求出OP的值，即可求出P的坐标。
练习册系列答案
学而优衔接教材南京大学出版社系列答案
小学课堂作业系列答案
金博士一点全通系列答案
相关题目
交于点B（2，1）．
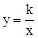的图象经过点（2，﹣1），则k的值为 ．
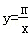的图象交于点A，与x轴交于点B，AC⊥x轴于点C，
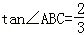，AB=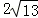
，OB=OC．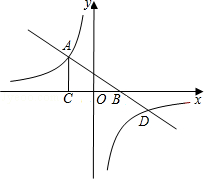
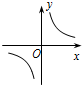
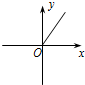
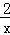的图象上，第二象限内的点B在反比例函数y=
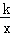的图象上，且OA⊥OB，cosA=
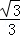，则k的值为（ ）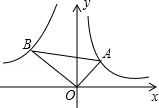
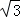
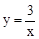和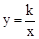
的部分图象如图所示，点C是y轴正半轴上一点，过点C作AB∥x轴分别交两个图象于点A、B．若CB=2CA，则k= ．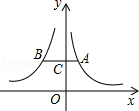
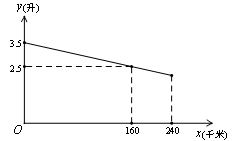
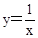（x＞0）的图象上，△P1OA1，△P2A1A2，△P3A2A3，…，△PnAn﹣1An都是等腰直角三角形，斜边OA1，A1A2，A2A3，…，An﹣1An都在x轴上（n是大于或等于2的正整数），则点P3的坐标是 ；点Pn的坐标是 （用含n的式子表示）．