题目内容
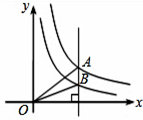
如图,在平面直角坐标系xOy中,一次函数y=kx+b与反比例函数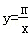 的图象交于点A,与x轴交于点B,AC⊥x轴于点C,
的图象交于点A,与x轴交于点B,AC⊥x轴于点C,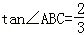 ,AB=
,AB=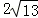 ,OB=OC.
,OB=OC.
(1)求反比例函数和一次函数的解析式;
(2)若一次函数与反比例函数的图象的另一交点为D,作DE⊥y轴于点E,连接OD,求△DOE的面积.
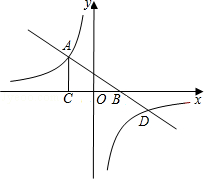
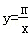 的图象交于点A,与x轴交于点B,AC⊥x轴于点C,
的图象交于点A,与x轴交于点B,AC⊥x轴于点C,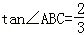 ,AB=
,AB=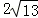 ,OB=OC.
,OB=OC.(1)求反比例函数和一次函数的解析式;
(2)若一次函数与反比例函数的图象的另一交点为D,作DE⊥y轴于点E,连接OD,求△DOE的面积.

(1)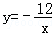 (2)6
(2)6
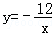 (2)6
(2)6试题分析:(1)在Rt△ABC中,利用勾股定理和锐角三角函数的定义求得AC=4,BC=6;然后由已知条件“OB=OC”求得点A、B的坐标;最后将其代入直线方程和反比例函数解析式,即利用待定系数法求函数的解析式;
(2)由反例函数y=
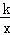 的几何意义可知,S△DOE=
的几何意义可知,S△DOE=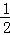 |k|.
|k|.解:(1)∵AC⊥x轴于点C,∴∠ACB=90°.
在Rt△ABC中,
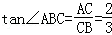 ,
,设 AC=2a,BC=3a,则
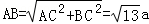 .
.∴
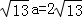 .
.解得:a=2.
∴AC=4,BC=6. …(2分)
又∵OB=OC,∴OB=OC=3.∴A(﹣3,4)、B(3,0). …(4分)
将A(﹣3,4)、B(3,0)代入y=kx+b,∴
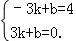
解得:
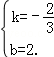 …(6分)
…(6分)∴直线AB的解析式为:
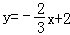 . …(7分)
. …(7分)将A(﹣3,4)代入
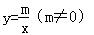 得:
得: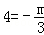 .解得:m=﹣12.
.解得:m=﹣12.∴反比例函数解析式为
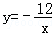 . …(8分)
. …(8分)(2)∵D是反比例函数
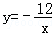 上的点,DE⊥y于点E,
上的点,DE⊥y于点E,∴由反例函数的几何意义,得S△DOE=
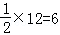 (10分)
(10分)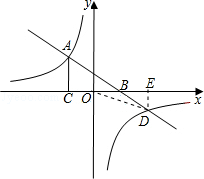
点评:此题主要考查了反比例函数与一次函数交点问题,关键掌握好利用图象求方程的解时,就是看两函数图象的交点横坐标.

练习册系列答案
 数学奥赛暑假天天练南京大学出版社系列答案
数学奥赛暑假天天练南京大学出版社系列答案 南大教辅抢先起跑暑假衔接教程南京大学出版社系列答案
南大教辅抢先起跑暑假衔接教程南京大学出版社系列答案
相关题目
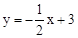 交AB,BC分别于点M,N,反比例函数
交AB,BC分别于点M,N,反比例函数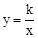 的图象经过点M,N.
的图象经过点M,N.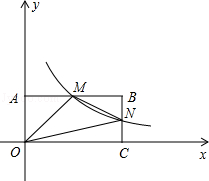
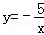 在第四象限的图象上的整点个数共有 个.
在第四象限的图象上的整点个数共有 个.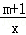 (x≠﹣1)的图象在第一象限内的交点为P(x0,3).
(x≠﹣1)的图象在第一象限内的交点为P(x0,3).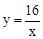 在第一象限内的图象上的一个点,以点P为顶点作等边△PAB,使A、B落在x轴上,则△POA的面积是
在第一象限内的图象上的一个点,以点P为顶点作等边△PAB,使A、B落在x轴上,则△POA的面积是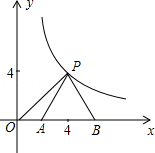
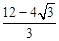 D.
D.
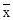 与人口数
与人口数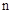 的函数关系图象是
的函数关系图象是

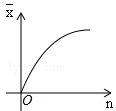

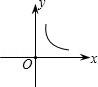
 ,
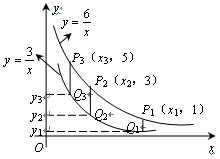
,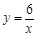 在第一象限内的图像如图所示,点
在第一象限内的图像如图所示,点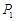 ,
,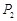 ,
,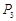 ,…,
,…,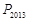 在函数
在函数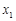 ,
,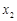 ,
,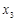 ,…,
,…,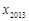 ,纵坐标分别是1,3,5,…,共2013个连续奇数,过点
,纵坐标分别是1,3,5,…,共2013个连续奇数,过点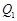 (
(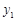 ),
), (
( ),
), (
( ),…,
),…, (
(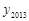 ),则
),则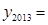 .
.
 在第一象限内如图所示作一条平行y轴的直线分别交双曲线于A、B两点,连OA、OB,则S△OAB= 。
在第一象限内如图所示作一条平行y轴的直线分别交双曲线于A、B两点,连OA、OB,则S△OAB= 。