题目内容
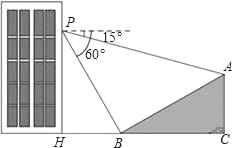
【题目】如图，小明在大楼30米高（即PH＝30米）的窗口P处进行观测，测得山坡上A处的俯角∠APQ为15°，山脚B处的俯角∠BPQ为60°，已知该山坡的坡度i（即tan∠ABC）为1：
，点P，H，B，C，A在同一个平面上，点H、B、C在同一条直线上，且PH丄HC．
（1）求出山坡坡角（∠ABC）的大小；
（2）求A、B两点间的距离（结果精确到0.1米，参考数据：≈1.732）．
【答案】（1）∠ABC＝30°；（2）AB≈34.6米．
【解析】
（1）根据俯角以及坡度的定义即可求解；
（2）在直角△PHB中，根据三角函数即可求得PB的长，然后在直角△PBA中利用三角函数即可求解．
解：（1）∵tan∠ABC＝1：
，
∴∠ABC＝30°；
（2）由题意得：∠PBH＝60°，
∵∠ABC＝30°，
∴∠ABP＝90°，
又∵∠APB＝45°，
∴△PAB为等腰直角三角形，
在直角△PHB中，PB＝
米．
在直角△PBA中，AB＝PB＝20
≈34.6米．
练习册系列答案
相关题目
