ƒøƒ⁄»ð
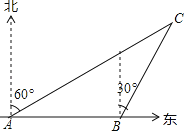
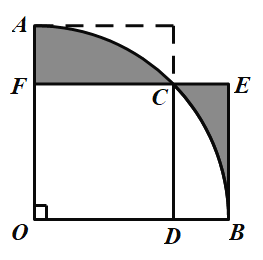
°æƒø°ø»ÁÕº1£¨≈◊ŒÔœþ![]() ”Î
”Î![]() ÷·Ωª”⁄
÷·Ωª”⁄![]() °¢
°¢![]() £¨Ωª
£¨Ωª![]() ÷·”⁄µ„
÷·”⁄µ„![]() £Æ
£Æ
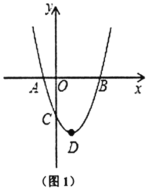
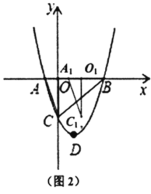
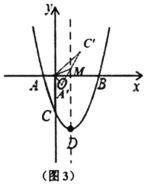
£®1£©≈◊ŒÔœþ∂•µ„![]() µƒ◊¯±ÍŒ™________£ª
µƒ◊¯±ÍŒ™________£ª
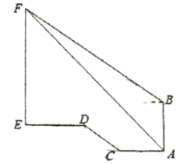
£®2£©»ÁÕº2£¨¡¨Ω”![]() °¢
°¢![]() £ÆΩ´
£ÆΩ´![]() —ÿ
—ÿ![]() ÷·∑ΩœÚ“‘√ø√Î1∏ˆµ•Œª≥§∂»µƒÀŸ∂»œÚ”“∆Ω“∆µ√µΩ
÷·∑ΩœÚ“‘√ø√Î1∏ˆµ•Œª≥§∂»µƒÀŸ∂»œÚ”“∆Ω“∆µ√µΩ![]() £¨‘À∂Ø ±º‰Œ™
£¨‘À∂Ø ±º‰Œ™![]() √ΣƵ±
√ΣƵ±![]() ±£¨«Û
±£¨«Û![]() ”Î
”Î![]() ÷ÿµ˛√ʪ˝
÷ÿµ˛√ʪ˝![]() ”Î
”Î![]() µƒ∫Ø ˝Ω‚Œˆ Ω£¨≤¢«Û≥ˆ
µƒ∫Ø ˝Ω‚Œˆ Ω£¨≤¢«Û≥ˆ![]() µƒ◊Ó¥Û÷µ£ª
µƒ◊Ó¥Û÷µ£ª
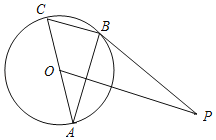
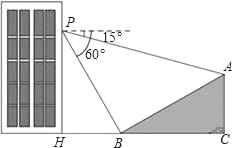
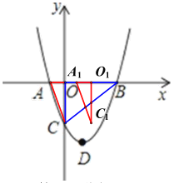
£®3£©»ÁÕº3÷–£¨Ω´![]() »∆µ„
»∆µ„![]() À≥ ±’Ζ˝◊™“ª∂®µƒΩ«∂»
À≥ ±’Ζ˝◊™“ª∂®µƒΩ«∂»![]() µ√µΩ
µ√µΩ![]() £¨±þ
£¨±þ![]() ”Î≈◊ŒÔœþµƒ∂‘≥∆÷·Ωª”⁄µ„
”Î≈◊ŒÔœþµƒ∂‘≥∆÷·Ωª”⁄µ„![]() £Æ‘⁄–˝◊™π˝≥Ã÷–£¨ «∑ҥʑ⁄“ªµ„
£Æ‘⁄–˝◊™π˝≥Ã÷–£¨ «∑ҥʑ⁄“ªµ„![]() £¨ πµ√
£¨ πµ√![]() £ø»Ù¥Ê‘⁄£¨÷±Ω”–¥≥ˆÀ˘”–¬˙◊„Ãıº˛µƒµ„
£ø»Ù¥Ê‘⁄£¨÷±Ω”–¥≥ˆÀ˘”–¬˙◊„Ãıº˛µƒµ„![]() µƒ◊¯±Í£ª»Ù≤ª¥Ê‘⁄£¨«ÎÀµ√˜¿Ì”…£Æ
µƒ◊¯±Í£ª»Ù≤ª¥Ê‘⁄£¨«ÎÀµ√˜¿Ì”…£Æ
°æ¥∞∏°ø£®1£©![]() µƒ◊¯±ÍŒ™
µƒ◊¯±ÍŒ™![]() £ª£®2£©µ±
£ª£®2£©µ±![]() ±£¨
±£¨![]() ”–◊Ó¥Û÷µ
”–◊Ó¥Û÷µ![]() £ª£®3£©
£ª£®3£©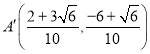 ªÚ
ªÚ
°æΩ‚Œˆ°ø
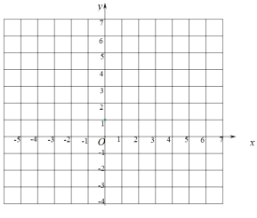
£®1£©∏˘æðµ„A∫Õµ„Bµƒ◊¯±Íø…µ√∂˛¥Œ∫Ø ˝µƒΩ‚Œˆ ΩŒ™![]() £¨»ª∫ÛΩ´∆‰ªØŒ™∂•µ„ Ωº¥ø…µ√≥ˆΩ·¬€£ª
£¨»ª∫ÛΩ´∆‰ªØŒ™∂•µ„ Ωº¥ø…µ√≥ˆΩ·¬€£ª
£®2£©∏˘æðtµƒ»°÷µ∑∂Œß∑÷¿ýÃ÷¬€£¨»ª∫Û¿˚”√![]() µƒ√ʪ˝ºı»•∆‰”ý∏˜»˝Ω«–Œµƒ√ʪ˝º¥ø…∑÷±«Û≥ˆ
µƒ√ʪ˝ºı»•∆‰”ý∏˜»˝Ω«–Œµƒ√ʪ˝º¥ø…∑÷±«Û≥ˆ![]() ”Î
”Î![]() µƒ∫Ø ˝Ω‚Œˆ Ω£¨»ª∫Û¿˚”√∂˛¥Œ∫Ø ˝µƒ–‘÷ «Û◊Ó÷µº¥ø…£ª
µƒ∫Ø ˝Ω‚Œˆ Ω£¨»ª∫Û¿˚”√∂˛¥Œ∫Ø ˝µƒ–‘÷ «Û◊Ó÷µº¥ø…£ª
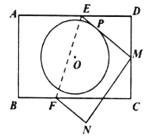
£®3£©»ÁÕº£¨…Ë![]() Œ™
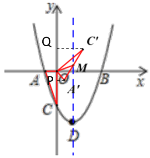
Œ™![]() £¨µ„MŒ™£®1£¨m£©£¨π˝µ„A°‰◊˜A°‰P°Õy÷·”⁄P,π˝µ„C°‰Q°Õy÷·”⁄Q£¨“◊÷§°˜A°‰PO°◊°˜OQC°‰£¨¡–≥ˆ±»¿˝ Ωº¥ø…«Û≥ˆµ„C°‰µƒ◊¯±Í£¨∏˘æð»˝Ω«–ŒÕ‚Ω«µƒ–‘÷ ∫Õµ»Ω«∂‘µ»±þø…÷§
£¨µ„MŒ™£®1£¨m£©£¨π˝µ„A°‰◊˜A°‰P°Õy÷·”⁄P,π˝µ„C°‰Q°Õy÷·”⁄Q£¨“◊÷§°˜A°‰PO°◊°˜OQC°‰£¨¡–≥ˆ±»¿˝ Ωº¥ø…«Û≥ˆµ„C°‰µƒ◊¯±Í£¨∏˘æð»˝Ω«–ŒÕ‚Ω«µƒ–‘÷ ∫Õµ»Ω«∂‘µ»±þø…÷§![]() Œ™
Œ™![]() µƒ÷–µ„£¨¿˚”√π¥π…∂®¿Ì«Û≥ˆµ„Mµƒ◊¯±Íº¥ø…«Û≥ˆµ„a∫Õb£¨¥”∂¯«Û≥ˆµ„A°‰µƒ◊¯±Í£Æ
µƒ÷–µ„£¨¿˚”√π¥π…∂®¿Ì«Û≥ˆµ„Mµƒ◊¯±Íº¥ø…«Û≥ˆµ„a∫Õb£¨¥”∂¯«Û≥ˆµ„A°‰µƒ◊¯±Í£Æ
£®1£©Ω‚£∫”…“—÷™≈◊ŒÔœþ”Î![]() ÷·Ωª”⁄
÷·Ωª”⁄![]() °¢
°¢![]() £¨
£¨
°ý∂˛¥Œ∫Ø ˝µƒΩ‚Œˆ ΩŒ™![]()
°ý![]() £¨
£¨
°ý∂•µ„![]() µƒ◊¯±ÍŒ™
µƒ◊¯±ÍŒ™![]() £Æ
£Æ
£®2£©Ω‚£∫µ±x=0 ±£¨y=-3
À˘“‘µ„Cµƒ◊¯±ÍŒ™£®0£¨-3£©
¢Ÿ»ÁÕº£¨µ±![]() ±£¨
±£¨
![]()
![]() £¨
£¨
°ýµ±![]() ±£¨
±£¨![]() ”–◊Ó¥Û÷µ
”–◊Ó¥Û÷µ![]() £ª
£ª
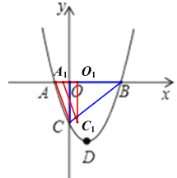
¢⁄»ÁÕº£¨µ±![]() ±£¨
±£¨![]() £¨
£¨
°ýµ±![]() ±£¨
±£¨![]() ”–◊Ó¥Û÷µ
”–◊Ó¥Û÷µ![]() £ª
£ª
°þ![]() £¨µ±
£¨µ±![]() ±£¨
±£¨![]() ”–◊Ó¥Û÷µ
”–◊Ó¥Û÷µ![]() £Æ
£Æ
£®3£©Ω‚£∫»ÁÕº£¨…Ë![]() Œ™
Œ™![]() £¨µ„MŒ™£®1£¨m£©£¨π˝µ„A°‰◊˜A°‰P°Õy÷·”⁄P,π˝µ„C°‰Q°Õy÷·”⁄Q£¨“◊÷§°˜A°‰PO°◊°˜OQC°‰
£¨µ„MŒ™£®1£¨m£©£¨π˝µ„A°‰◊˜A°‰P°Õy÷·”⁄P,π˝µ„C°‰Q°Õy÷·”⁄Q£¨“◊÷§°˜A°‰PO°◊°˜OQC°‰
°ý![]()
ø…µ√![]() £Æ
£Æ
–˝◊™π˝≥Ã÷–£¨»Ù¥Ê‘⁄“ªµ„![]() πµ√
πµ√![]() £¨‘Ú
£¨‘Ú![]() Œ™
Œ™![]() µƒ÷–µ„£¨
µƒ÷–µ„£¨
°þ![]() £¨
£¨
°ý![]() £Æ
£Æ
°ý![]()
Ω‚µ√£∫m=![]()
°ý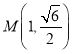 ªÚ
ªÚ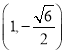
°ý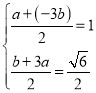 ªÚ
ªÚ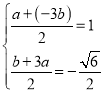
Ω‚µ√£∫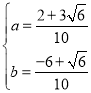 ªÚ
ªÚ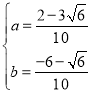
°ý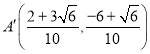 ªÚ
ªÚ £Æ
£Æ

 ø⁄À„–ƒÀ„ÀŸÀ„”¶”√Âœµ¡–¥∞∏
ø⁄À„–ƒÀ„ÀŸÀ„”¶”√Âœµ¡–¥∞∏ Õ¨≤ΩÕÿ’π‘ƒ∂¡œµ¡–¥∞∏
Õ¨≤ΩÕÿ’π‘ƒ∂¡œµ¡–¥∞∏°æƒø°ø°∞Õ∆Ω¯»´ø∆‘ƒ∂¡£¨≈ý”˝ ±¥˙–¬»À°±£Æƒ≥—ß–£Œ™¡À∏¸∫√µÿø™’π—ß…˙∂¡ ȪÓ∂Ø£¨Àʪ˙µ˜≤È¡Àæ≈ƒÍº∂50√˚—ß…˙◊ÓΩ¸“ª÷еƒ∂¡ È ±º‰£¨Õ≥º∆ ˝æð»Áœ¬±Ì£∫
±º‰£®–° ±£© | 6 | 7 | 8 | 9 | 10 |
»À ˝ | 5 | 8 | 12 | 15 | 10 |
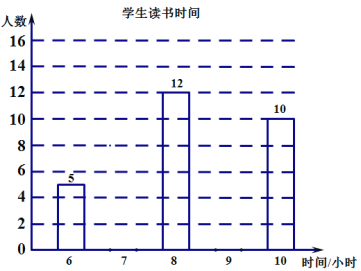
£®1£©∏˘æð…œ ˆ±Ì∏Ò≤π»´œ¬√ʵƒÃı–ŒÕ≥º∆Õº£ª
£®2£©–¥≥ˆ’‚50√˚—ß…˙∂¡ È ±º‰µƒ÷⁄ ˝°¢÷–Œª ˝°¢∆Ωæ˘ ˝£ª
£®3£©»Ù∏√–£”–1000√˚—ß…˙£¨«Û◊ÓΩ¸“ª÷еƒ∂¡ È ±º‰≤ª…Ÿ”⁄7–° ±µƒ»À ˝£ø