题目内容
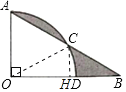
【题目】如图，∠AOB＝90°，∠B＝30°，以点O为圆心，OA为半径作弧交AB于点C，交OB于点D，若OA＝4，则阴影部分的面积为_____．
【答案】
π．
【解析】
连接OC，作CH⊥OB于H，根据直角三角形的性质求出AB，根据勾股定理求出BD，证明△AOC为等边三角形，得到∠AOC＝60°，∠COB＝30°，根据扇形面积公式、三角形面积公式计算即可．
解：连接OC，作CH⊥OB于H，
∵∠AOB＝90°，∠B＝30°，
∴∠OAB＝60°，AB＝2OA＝8，
由勾股定理得，OB＝
＝
，
∵OA＝OC，∠OAB＝60°，
∴△AOC为等边三角形，
∴∠AOC＝60°，
∴∠COB＝30°，
∴CO＝CB，CH＝
OC＝2，
∴阴影部分的面积＝
﹣×4×4×
+××2﹣
＝π，
故答案为：π．
练习册系列答案
相关题目
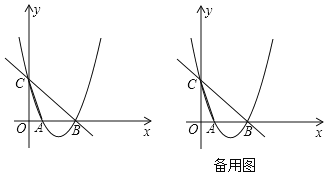
【题目】某蔬菜市场为指导某种蔬菜的生产和销售，对往年的市场行情和生产情况进行了调查，提供的信息如下：
信息1：售价和月份满足一次函数关系，如下表所示．
月份 | … | 3 | 6 | … |
售价 | … | 5 | 3 | … |
信息2：成本和月份满足二次函数关系，并且知道该种蔬菜在6月成本达到最低为1元/千克，9月成本为4元/千克．
根据以上信息回答下列问题：
（1）在7月，这种蔬菜的成本是多少元每千克？
（2）在过去的一年中，某商家平均每天卖出
该种蔬菜，则哪个月的利润最大，最大利润为多少？（一个月按30天计算）
