题目内容
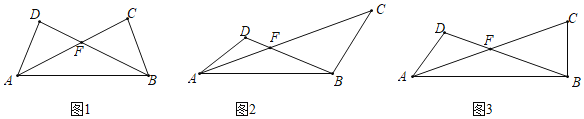
【题目】如图，在菱形ABCD中，过点A作AH⊥BC，分别交BD，BC于点E，H，F为ED的中点，∠BAF＝120°，则∠C的度数为_____．
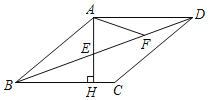
【答案】140°
【解析】
根据菱形的性质得出AD∥BC，∠ABD＝∠CBD，进而利用三角形的内角和解答即可．
解：设∠CBD＝x，
∵四边形ABCD为菱形，
∴AD∥BC，∠ABD＝∠CBD＝x，
∴∠ADB＝∠CBD＝x，
∵AH⊥BC，AD∥BC，
∴∠DAH＝∠AHB＝90°，
∵F为ED的中点．
∴AF＝FD，
∴∠FAD＝∠ADB＝x，
∵∠BAF＝120°，
∴∠BAD＝120°+x，
∵AD∥BC，
∴∠BAD+∠ABC＝180°，
可得：2x+120°+x＝180°，
解得：x＝20°，
∴∠BAD＝120°+x＝140°
∵四边形ABCD为菱形，
∴∠C＝∠BAD＝140°．
故答案为：140°．
练习册系列答案
相关题目
【题目】小魏探究学习函数的经验，对函数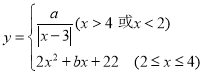
的图像与性质进行了研究，下面是小魏的探究过程，请补充完整．
（1）下表是
与
的几组对应值：
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
请直接写出：
_______，
______，
_______．
（2）画出该函数图像．
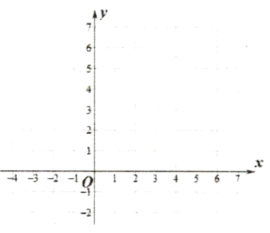
（3）写出该函数的一条性质：_______________．
（4）一次函数
与该函数图像至少有三个交点，则
的范围_______．
