题目内容
【题目】如图,一张三角形纸片ABC,其中∠C=90°,AC=4,BC=3.现小林将纸片做三次折叠:第一次使点A落在C处;将纸片展平做第二次折叠,使点B落在C处;再将纸片展平做第三次折叠,使点A落在B处.这三次折叠的折痕长依次记为a,b,c,则a,b,c的大小关系是( ) 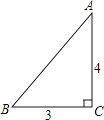
A.c>a>b
B.b>a>c
C.c>b>a
D.b>c>a
【答案】D
【解析】解:第一次折叠如图1,折痕为DE,由折叠得:AE=EC= ![]() AC=
AC= ![]() ×4=2,DE⊥AC
×4=2,DE⊥AC
∵∠ACB=90°
∴DE∥BC
∴a=DE= ![]() BC=
BC= ![]() ×3=
×3= ![]()
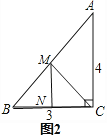
第二次折叠如图2,折痕为MN,
由折叠得:BN=NC= ![]() BC=
BC= ![]() ×3=
×3= ![]() ,MN⊥BC
,MN⊥BC
∵∠ACB=90°
∴MN∥AC
∴b=MN= ![]() AC=
AC= ![]() ×4=2
×4=2
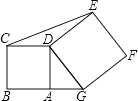
第三次折叠如图3,折痕为GH,
由勾股定理得:AB= ![]() =5由折叠得:AG=BG=
=5由折叠得:AG=BG= ![]() AB=
AB= ![]() ×5=
×5= ![]() ,GH⊥AB
,GH⊥AB
∴∠AGH=90°
∵∠A=∠A,∠AGH=∠ACB
∴△ACB∽△AGH
∴ ![]() =
= ![]() ∴
∴ ![]() =
= ![]() ∴GH=
∴GH= ![]() ,即c=
,即c= ![]() ∵2>
∵2> ![]() >
> ![]()
∴b>c>a
故选D.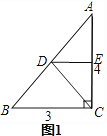
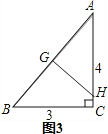
(1)图1,根据折叠得:DE是线段AC的垂直平分线,由中位线定理的推论可知:DE是△ABC的中位线,得出DE的长,即a的长;
(2)图2,同理可得:MN是△ABC的中位线,得出MN的长,即b的长;
(3)图3,根据折叠得:GH是线段AB的垂直平分线,得出AG的长,再利用两角对应相等证△ACB∽△AGH,利用比例式可求GH的长,即c的长.本题考查了折叠的问题,折叠是一种对称变换,它属于轴对称,折叠前后图形的形状和大小不变,位置变化,对应边和对应角相等.本题的关键是明确折痕是所折线段的垂直平分线,准确找出中位线,利用经过三角形一边中点与另一边平行的直线必平分第三边这一性质得出对应折痕的长,没有中位线的可以考虑用三角形相似来解决.