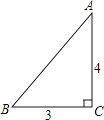
题目内容
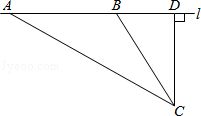
【题目】如图,四边形ABCD是矩形,点E在CD边上,点F在DC延长线上,AE=BF．
（1）求证：四边形ABFE是平行四边形；
（2）若∠BEF=∠DAE,AE=3,BE=4,求EF的长．
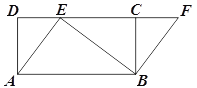
【答案】（1）证明见解析（2）EF=AB=5．
【解析】（1）证明：∵四边形ABCD是矩形，∴AD=BC，∠D=∠BCD=90°．
∴∠BCF=180°﹣∠BCD=180°﹣90°=90°．
∴∠D=∠BCF．在Rt△ADE和Rt△BCF中，
∴Rt△ADE≌Rt△BCF．
∴∠1=∠F．∴AE∥BF．∵AE=BF，∴四边形ABFE是平行四边形．
（2）解：∵∠D=90°，∴∠DAE+∠1=90°．∵∠BEF=∠DAE，∴∠BEF+∠1=90°．
∵∠BEF+∠1+∠AEB=180°，∴∠AEB=90°．
在Rt△ABE中，AE=3，BE=4，AB=
．
∵四边形ABFE是平行四边形，∴EF=AB=5．
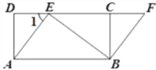
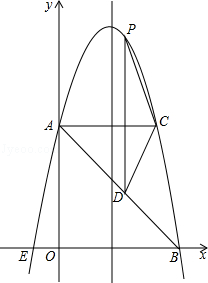
【题目】如图，关于x的二次函数y=x2﹣x+m的图象交x轴的正半轴于A，B两点，交y轴的正半轴于C点，如果x=a时，y＜0，那么关于x的一次函数y=（a﹣1）x+m的图象可能是（ ） 
A.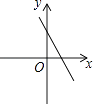
B.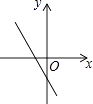
C.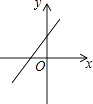
D.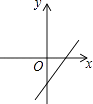
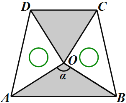
【题目】如图1，将边长为1的正方形ABCD压扁为边长为1的菱形ABCD．在菱形ABCD中，∠A的大小为α，面积记为S．
（1）请补全下表：
30° | 45° | 60° | 90° | 120° | 135° | 150° | |
S |
| 1 |
|
（2）填空：
由（1）可以发现正方形在压扁的过程中，菱形的面积随着∠A大小的变化而变化，不妨把菱形的面积S记为S(α)．例如：当α＝30°时，
；当α＝135°时，
．由上表可以得到
( ______°)；
( ______°)，…，由此可以归纳出
．
（3） 两块相同的等腰直角三角板按如图的方式放置，AD＝
，∠AOB＝α，试探究图中两个带阴影的三角形面积是否相等，并说明理由（注：可以利用（2）中的结论）．
