题目内容
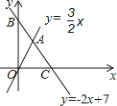
【题目】如图,直线l1过点A(0,4),点D(4,0),直线l2:![]() 与x轴交于点C,两直线
与x轴交于点C,两直线![]() ,
,![]() 相交于点B.
相交于点B.
(1)求直线![]() 的解析式和点B的坐标;
的解析式和点B的坐标;
(2)求△ABC的面积.

【答案】(1)直线![]() 的解析式为y=-x+4,点B的坐标为(2,2);(2)
的解析式为y=-x+4,点B的坐标为(2,2);(2)![]() .
.
【解析】(1)根据题意l1经过A、B两点,又直线的解析式为y=ax+b,代入可得a、b的值.
(2)由图可知△ACB的面积为△ACD与△CBD的差,所以求得△ACD与△BCD的面积即可知△ACB的面积.
(1)设l1的解析式为:y=ax+b.
∵l1经过A(0,4),D(4,0),
∴将A、D代入解析式得:b=4,4a+b=0,
∴a=﹣1,b=4.
即l1的解析式为:y=﹣x+4,
l1与l2联立 ,得:B(2,2);
,得:B(2,2);
(2)C是l2与x轴的交点,在y=![]() x+1中所以令y=0,得:C(﹣2,0),
x+1中所以令y=0,得:C(﹣2,0),
∴|CD|=6,|AO|=4,B到x轴的距离为2.
∵AO⊥CD,
∴△ACD的面积为![]() |AO||CD|=
|AO||CD|=![]() ×4×6=12 ,
×4×6=12 ,
△CBD的面积为![]() ×B到x轴的距离×CD=
×B到x轴的距离×CD=![]() ×2×6=6 ,
×2×6=6 ,
∴△ABC的面积=△ACD的面积-△CBD的面积=6.

练习册系列答案
 小学课时特训系列答案
小学课时特训系列答案
相关题目