Question

如图，在□ABCD中，点E，F分别在AB、CD上，且AE＝CF． (1)求证：△ADE≌△CBF． (2)若DF＝BF，求证：四边形DEBF是菱形．

Answer 1

答案：
解析：

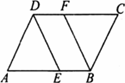
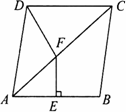
证明：(1)∵四边形ABCD是平行四边形， 　　∴AD＝BC，∠A＝∠C， 　　在△ADE和△CBF中， 　　∵ 　　∴△ADE≌△CBF． 　　(2)∵四边形ABCD是平行四边形， 　　∴AB∥CD，AB＝CD． 　　又∵AE＝CF， 　　∴DF＝EB， 　　∴四边形DEBF是平行四边形． 　　又∵DF＝FB， 　　∴四边形DEBF是菱形．